THE relative position between two figures is the study of the possibilities of relationship between geometric figures within a given space. It is not necessary for this space to be three-dimensional. In plane geometry, all geometric figures belong to a space that we usually call a plane.
When looking at the plane as an object belonging to space, this space must have at least one dimension more than the plane. Thus, as the plane is an object that has two dimensions, the analysis of relative positions between other objects any of this plane must be made, at least, in three-dimensional space.
Any line has three possibilities of interaction with the plane. These possibilities are known as relative positions between a line and a plane and are listed below:
Line contained in the plane
We say that a straight is contained in the plane when all your points are also points on the plane. It is also possible to say that the plane contains the line. The language is the same as used for numerical sets.
What guarantees that a straight line is contained in the plane is the postulate of inclusion, which states the following:
If a plane contains two points of a line, then the entire line is contained in that plane. This fact cannot be proved, but it must be accepted as true, as it composes the foundations of Geometry. That's why it's called postulate or axiom.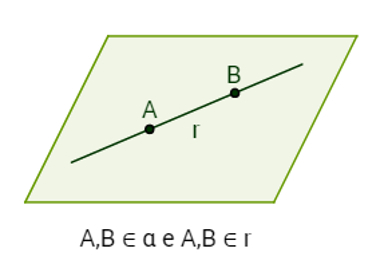
Line r belonging (contained) to plane α
Line and plane competing
Also called drying, this position refers to a line and a plane that have a single point in common. This fact is guaranteed by the postulate of existence, which says: There are infinite points within a plane as well as outside of it. As this postulate guarantees the existence of at least one point in the plane and one outside it, through the postulate of determination, we can say that: two distinct points determine a single line that passes through them, thus, we prove the existence of a line that has only one point common to the flat.
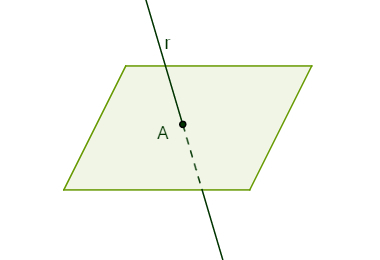
Straight r concurrent (or secant) to the α plane
A line secant to a plane through point A and which forms an angle of 90° with any line belonging to that plane that contains point A is called a line. perpendicular (or orthogonal) to the plane.
Parallel straight and plane
Line and plane are parallel when they have no common ground.
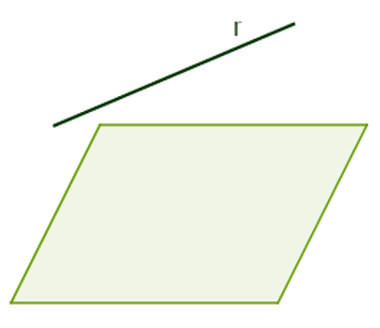
Line r parallel to plane α
Keeping in mind Euclid's fifth postulate (given a straight line and a point not belonging to it, through the point passes a single line parallel to the given line), it is possible to conclude the following property of parallelism between line and flat: If a line r does not belong or is concurrent with the plane α, but is parallel to a line s contained in that plane, then the line r is parallel to the plane α.
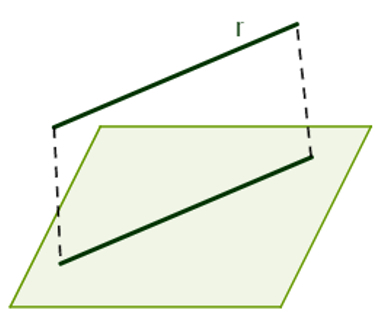
Line r is parallel to line s, which belongs to plane α, so r is parallel to α
By Luiz Paulo Moreira
Graduated in Mathematics
Source: Brazil School - https://brasilescola.uol.com.br/matematica/posicao-relativa-entre-reta-plano.htm


