System of equations: how to calculate, methods, exercises – brazil school

We consider a system of equations when we are going to solve problems that involve numerical quantities and that, generally, we resort to the use of equations to represent such situations. In most real problems, we should consider more than one equation simultaneously, which thus depends on the design of systems.

Problems such as traffic shaping can be solved using linear systems. we must understand the elements of a linear system, what methods to use and how to determine its solution.

Systems of equations are those that work with more than one numerical quantity.

Equations

Our study will be around systems of linear equations, so let's first understand what a linear equation.

An equation will be called linear when it can be written this way:

The₁ ·x₁ + the₂ ·x₂ + the₃ ·x₃ +...+ to_no ·x_no = k

In which (the_1, The_2, The_3,..., The_no) they are the coefficients of the equation, (x_1, x_2, x_3,..., x_no) are the incognitos and must be linear and k is the termindependent.

• Examples

• -2x + 1 = -8 ® Linear equation with one unknown
• 5p + 2r =5 ® Linear equation with two unknowns
• 9x – y - z = 0 ® Linear equation with three unknowns
• 8ab +c – d = -9 ® Nonlinear Equation

Know more: Differences between function and equation

How to calculate a system of equations?

The solution of a linear system is every ordered and finite set that satisfies all the equations of the system at the same time. The number of elements of the solution set is always equal to the number of unknowns in the system.

• Example

Consider the system:

The ordered pair (6; -2) satisfies both equations, so it is the solution of the system. The set formed by the system's solutions is called solution set. From the example above, we have:

S = {(6; -2)}

The way of writing with braces and parentheses indicates a solution set (always between braces) formed by an ordered pair (always between parentheses).

Observation: If two or more systems have the same set solution, these systems are called equivalent systems.

Replacement method

The replacement method boils down to following three steps. For this, consider the system

• Step 1

The first step is to choose one of the equations (the easiest) and isolate one of the unknowns (the easiest). Thus,

x – 2y = -7

x = -7 + 2y

• Step 2

In the second step, just replace, in the unchosen equation, the unknown isolated in the first step. Soon,

3x + 2y = -7

3 (-7 + 2y) + 2y = - 5

-21 +6y + 2y =-5

8y = -5 +21

8y = 16

y = 2

• Step 3

The third step, consists of replace found value in the second step in any of the equations. Thus,

x = -7 + 2y

x = -7 + 2(2)

x = -7 +4

x = -3

Therefore, the system solution is S {(-3, 2)}.

addition method

To perform the addition method, we must remember that the coefficients of one of the unknowns must be opposite, that is, having equal numbers with opposite signs. Let's consider the same system as the method of substitution.

See that the unknown coefficients y meet our condition, so it is enough to add each one of the columns of the system, obtaining the equation:

4x + 0y = -12

4x = -12

x = -3

And substituting the value of x in any of the equations we have:

x - 2y = -7

-3 - 2y = -7

-2y = -7 + 3

(-1) (-2y) = -4 (-1)

2y = 4

y = 2

Therefore, the solution of the system is S {(-3, 2)}

Read too: Problem solving by equation systems

Classification of linear systems

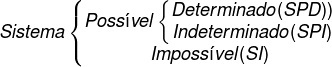
We can classify a linear system by the number of solutions. A linear system can be classified into possible and determined, possible andindeterminate and impossible.

→ System is possible and determined (SPD): unique solution

→ Possible and indeterminate system (SPI): more than one solution

→ Impossible system: no solution

See the scheme:

Exercise solved

Question 1 - (Vunesp) A mechanical pencil, three notebooks and a pen cost 33 reais together. Two mechanical pencils, seven notebooks and two pens cost 76 reais together. The cost of a mechanical pencil, a notebook and a pen, together, in reais is:

a) 11

b) 12

c) 13

d) 17

e) 38

Solution

Let's assign the unknown x at the price of each mechanical pencil, y at the price of each notebook and z at the price of each pen. From the statement, we have to:

Multiplying the top equation by -2 we have to:

Adding term to term, we will have to:

y = 10

Replacing the value of y found in the first equation, we have to:

x + 3y + z = 33

x + 30 + z = 33

x + z = 3

Therefore, the price of a pencil, a notebook and a pen is:

x + y + z = 13 reais.

Alternative C

by Robson Luiz
Maths teacher

Source: Brazil School - https://brasilescola.uol.com.br/matematica/sistema-duas-equacoes.htm