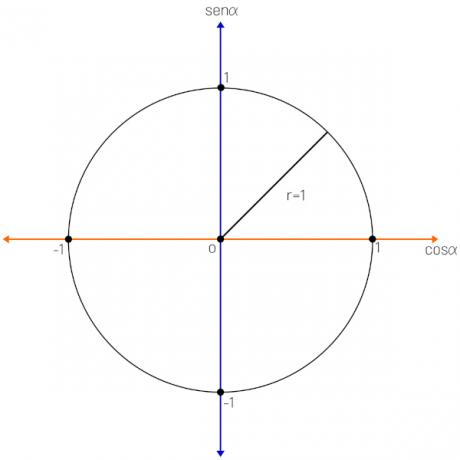
the trigonometric circle is a circle of radius 1 represented in the Cartesian plane. In it, the horizontal axis is the cosine axis and the vertical axis is the sine axis. It can also be called a trigonometric cycle.
It is used to carry out the study of trigonometric ratios. With it, it is possible to better understand the main trigonometric reasons for angles greater than 180º, namely: the sine, the cosine and the tangent.
Read too: 4 most common mistakes in Basic Trigonometry
Step by step to build the trigonometric circle
To construct the trigonometric circle, we use two axes, one vertical and one horizontal, like a Cartesian plane. The horizontal axis is known as cosine axis, and the vertical axis is known as sine axis.

With the construction of the axes, let's draw the graph of a circle that has radius 1.
Trigonometric ratios in the circle
We use the circle to find the value of
sine, cosine and tangent, according to the angle value. having in vertical axis the sine value and on the horizontal axis the cosine value, by determining an angle on the trigonometric circle, it is possible to find the value of sine and cosine by analyzing the coordinates of the point where the line segment connects the center of the circle and the circumference, represented by P in the image a follow. If we draw the tangent line to the circle at the point (1.0), we can also calculate the tangent of this angle analytically according to the image: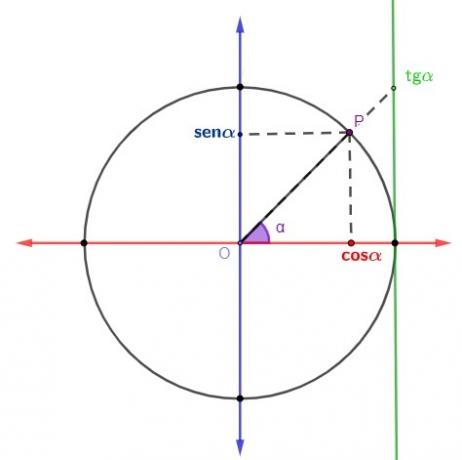
Read too: What are secant, cosecant and cotangent?
Trigonometric Circle Radians
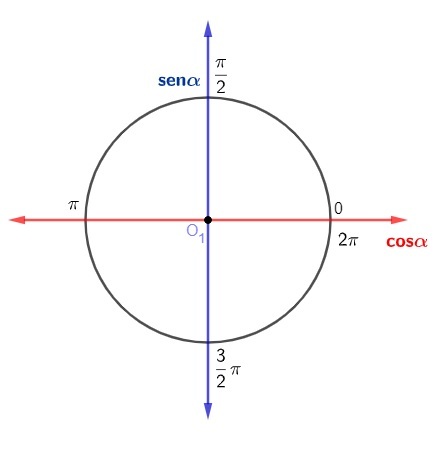
We know that an arc can be measured using two different measurement units: the measure in degrees and the measure in radians. We know that the circumference is 360º and that the length of your arc is 2π:
Quadrants of the trigonometric circle
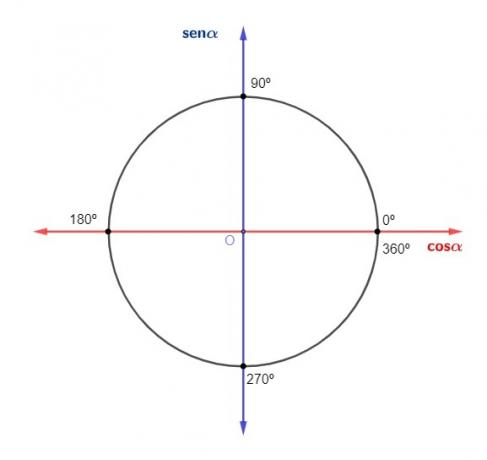
Whether in radians or degrees, it is possible to define the quadrant in which a given arc is located according to its measurement.
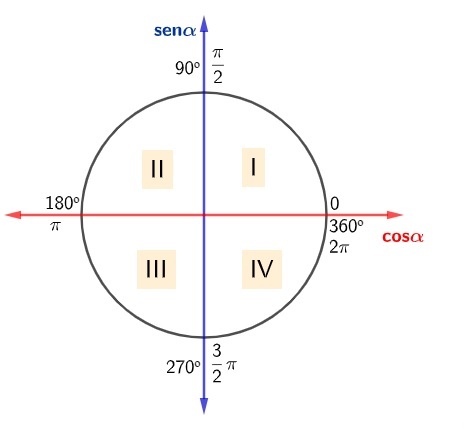
Analyzing the cycle, we have to:
first quadrant: angles that are between 0 to 90° or 0 and π/2 radians;
second quadrant: angles that are between 90º and 180º or π/2 and π radians;
third quadrant: angles that are between 180º and 270º or π and 3 π/2 radians;
fourth quadrant: angles that are between 270° and 360° or 3π/2 and 2π radians.
Read too: Plan characteristics and properties
Remarkable angles in the trigonometric circle
At the beginning of the study of trigonometry, we learned that the notable angles are the angles of 30º, 45º and 60º, which have the value of the known sine, cosine and tangent. However, due to the symmetry of the trigonometric cycle, it is possible to find the sine and cosine values for these angles and the symmetric angles to him in each of the quadrants.

Trigonometric Circle Signs
To understand what is the sign of each of the trigonometric ratios in the cycle, it is enough to analyze the axis values in the Cartesian plane.
Let's start with the cosine. Since it is the horizontal axis, the cosine of angles included to the right of the vertical axis is positive, and the cosine of angles included to the left of the vertical axis is negative.
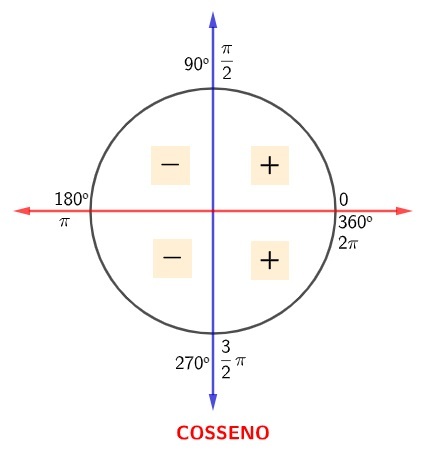
Now, to understand the sine sign of an angle, just remember that the vertical axis is the sine axis, so the sine of an angle that is above the horizontal axis is positive; but if the angle is below the horizontal axis, the sine of this angle is negative, as shown in the following image:
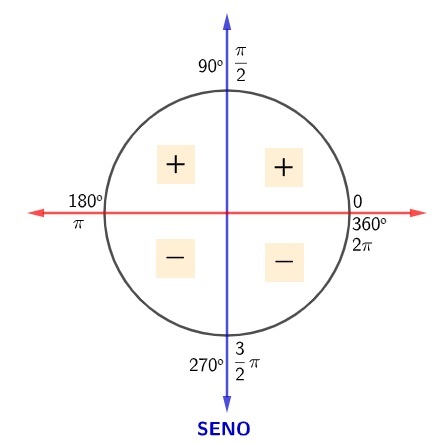
We know that the tangent is the ratio between the sine and the cosine, then, to find the sign of the tangent for each of the quadrants, we play the sign game, which makes the tangent positive in the odd quadrants and negative in the even quadrants:
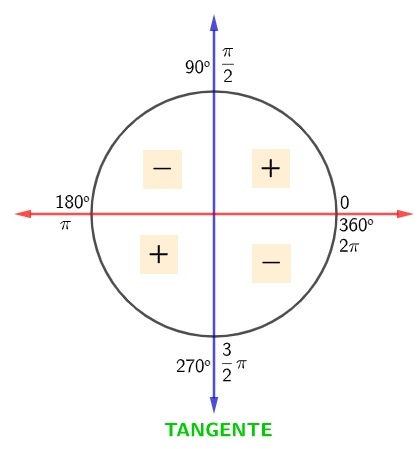
Read too: What are semi-straight, semi-plane and semi-space?
symmetry in the circle
Analyzing the trigonometric cycle, it is possible to construct a way to reduce the sine, cosine and tangent to the first quadrant. This reduction means finding in the first quadrant an angle that is symmetrical to an angle of the other quadrants, because, when we work with a symmetric angle, the value of the trigonometric ratios is the same, changing only its signal.
Reduction of an angle that is in the 2nd quadrant to the 1st quadrant
Starting with the angles that are in the 2nd quadrant, we have to:
As we know, in the 1st and 2nd quadrants, sine is positive. So, to calculate the reduction of sine from the 2nd quadrant to the 1st quadrant, we use the formula:
sin x= sin (180º - x)
The cosine and tangent in the 2nd quadrant are negative. To reduce the cosine from the 2nd quadrant to the 1st quadrant, we use the formula:
cosx = – cos (180º – x)
tg x = – tg (180º – x)
Example:
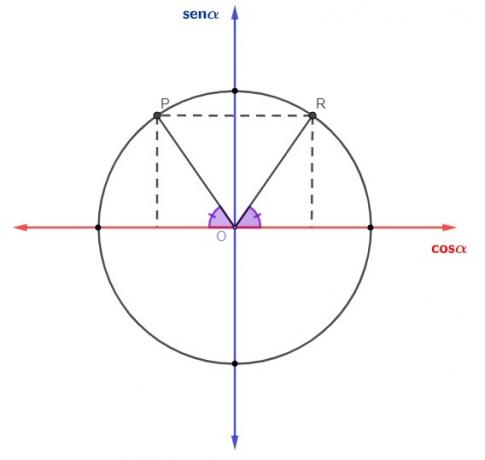
What is the value of the sine and cosine of an angle of 120°?
The 120° angle is a quadrant second angle as it is between 90° and 180°. To reduce this angle to the 1st quadrant, we calculate:
sin 120° = sin (180° – 120°)
sin 120º = sin 60º
The 60° angle is a remarkable angle, so its sine value is known, so:

Now let's calculate your cosine:
cos 120º = – cos (180 – 120)
cos 120º = - cos 60º
As we know the cosine of 60º, we have to:
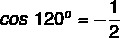
Reduction of an angle that is in the 3rd quadrant to the 1st quadrant
As in the 2nd quadrant, there is symmetry between angles in the 3rd quadrant and angles in the 1st quadrant.
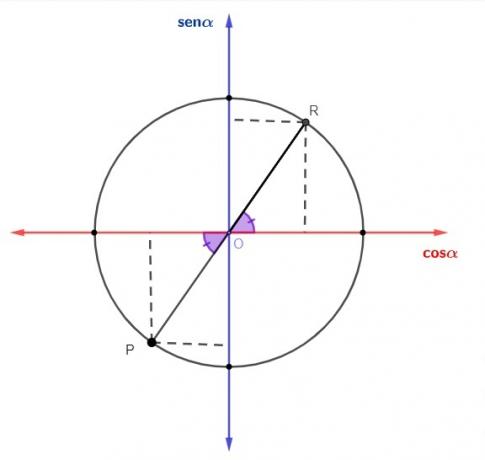
The sine and cosine in the third quadrant are negative. So, to reduce sine and cosine from the 3rd quadrant to the 1st quadrant, we use the formula:
sin x = – sin (x – 180º)
cosx = – cos (x – 180º)
The tangent in the 3rd quadrant is positive. To reduce it, we use the formula:
tg x = tg (x – 180º)
Example:
Calculate the sine, cosine, and tangent of 225º.
sin 225º = – sin (225º – 180º)
sin 225º = – sin 45º
As 45º is a remarkable angle, when consulting the table, we have to:
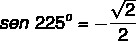
Now, calculating the cosine, we have to:
tg 225º = tg (225º - 180º)
tg 225º = tg 45º
We know that tg45º = 1, so:
tg 225º = 1
Reduction of an angle that is in the 4th quadrant to the 1st quadrant
With the same reasoning as the previous reductions, there is a symmetry between the 4th and 1st quadrant:
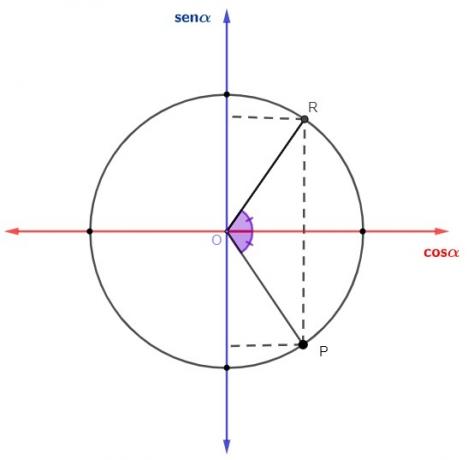
The sine and tangent values in the 4th quadrant are negative. So, to make the reduction from the 4th to the 1st quadrant, we use the formula:
sin x = – sin (360º – x)
tg x = – tg (360º – x)
The cosine in the 4th quadrant is positive. So, to reduce to the 1st quadrant, the formula is:
cos x = cos (360º - x)
Example:
Calculate the value of sine and cosine of 330º.
Starting with the sine:
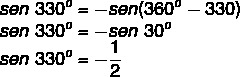
Now calculating the cosine:
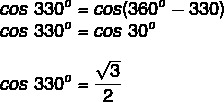
Read too: How to calculate distance between two points in space?
Trigonometric Circle Solved Exercises
question 1 - During the study of the circular moment, a physicist analyzed an object that was rotating around itself, forming an angle of 15,240º. Analyzing this angle, the arc formed by it is in:
A) quadrant I.
B) quadrant II.
C) quadrant III.
D) quadrant IV.
E) on top of one of the axes.
Resolution
Alternative B.
We know that every 360° this object has completed a circle around itself. When performing the division of 15,240 by 360, we'll find how many complete turns this object has made around itself, but our main interest is in the rest, which represents the angle at which it stopped.
15.240: 360 = 42,333…
The result shows that he did 42 turns around himself, but 360 · 42 = 15.120, so he left an angle of:
15.240 – 15.120 = 120º
We know that 120° is a quadrant second angle.
Question 2 - Please judge the following statements:
I → When calculating tg 140º, the value will be negative.
II → The 200° angle is an angle of the 2nd quadrant.
III → Sen 130º = sin 50º.
Mark the correct alternative:
A) Only I is false.
B) Only II is false.
C) Only III is false.
D) All are true.
Resolution
Alternative B.
I → True, since the 140º angle belongs to the 2nd quadrant, in which the tangent is always negative.
II → False, as the 200° angle is an angle of the 3rd quadrant.
III → True, because to reduce an angle from the 2nd to the 1st quadrant, just calculate the difference of 180° – x, then:
sin 130° = sin (180° – 130°)
sin 130th = sin 50th
By Raul Rodrigues de Oliveira
Maths teacher
Source: Brazil School - https://brasilescola.uol.com.br/matematica/simetria-no-circulo-trigonometrico.htm
