We know how repeat arrangement, or complete arrangement, all the ordered regroupings that we can form with k elements of a set with no elements, with an element of no may appear more than once. THE combinatorial analysis is the area of mathematics that develops counting techniques to find the amount of possibilities for groupings in certain situations.
Among these groupings, there is the arrangement with repetition, present, for example, in the creating passwords, license plates, between others. To solve these situations, we apply the arrangement formula with repetition as a counting technique. There are different formulas for calculating the repeating arrangement and the non-repeating arrangement, so it is important to know how to differentiate each of these situations in order to apply the correct counting technique.
Read too: Fundamental principle of counting - main concept of combinatorial analysis
What is arrangement with repetition?
![There is an arrangement with repetition in the production of vehicle plates. [1]](/f/46a11aed3d571c029896ad4272473301.jpg)
In our daily lives, we come across situations that involve sequences and groupings, which appear in the choose passwords from social networks or bank, and also in phone numbers or situations that involve queues. Anyway, we are surrounded by situations that involve these groupings.
For example, on license plates, which are made up of three letters and four numbers, there is a unique string by state that identifies each of the cars, in this case, we are working with arrangements. When it is possible to repeat the elements, we are working with the complete arrangement or arrangement with repetition.
Given a set with no elements, we know as arrangement with repetition all the groupings that we can form with k elements of this set, where an element can be repeated more than once. On vehicle license plates, for example, it is the number of possible license plates that we can form, taking taking into account that they have three letters and four numbers and that the letters and numbers can be repeated.
To calculate the number of possible repeating arrangements, we use a very simple formula.
Do not stop now... There's more after the advertising ;)
Arrangement formula with repetition
To find the full arrangement amount of no distinct elements taken from k in
oh, in a given situation that allows repetition of an element, we use the following formula:
AIRno,k = nok
AR → arrangement with repetition
no → number of elements in the set
k → number of elements that will be chosen
See too: Simple combination - count all subsets of a given set
How to calculate the repeating arrangement number
To better understand how to apply the repeat arrangement formula, see the example below.
Example 1:
A bank password has five digits made up exclusively of numbers, what is the number of possible passwords?
We know that the password is a five-digit string and that there is no restriction on repetitions, so we will apply the arrangement formula with repetition. The user has to choose, among 10 digits, which will compose each of the five digits of this password, that is, we want to calculate the arrangement with repetition of 10 elements taken every five.
AIR10,5 = 105 = 10.000
So there are 10,000 password possibilities.
Example 2:
Knowing that vehicle license plates are made up of three letters and four numbers, how many license plates is it possible to form?
Our alphabet consists of 26 letters, and there are 10 possible numbers, so let's split into two complete arrays and find the number of possible arrays for the letters and numbers.
AIR26,3 = 26³ = 17.576
AIR10,4 = 104 = 10.000
Thus, the total of possible arrangements is:
17.576 · 10.000 = 1.757.600.000
Difference between simple arrangement and repeat arrangement
Differentiating the simple arrangement from the arrangement with repetition is essential for solving problems on the topic. The important thing for differentiation is to realize that, when we are dealing with a situation in which there are regroupings whose order is important, it is about of an arrangement, and if these regroupings allow repetition between terms, it is an arrangement with repetition, also known as arrangement complete. When the regrouping does not allow repetition, its about a simple arrangement.
The formula for the simple arrangement is different from the one we use for the repeat arrangement.

We've seen examples of repeating arrangement earlier, now see an example of simple arrangement
Example:
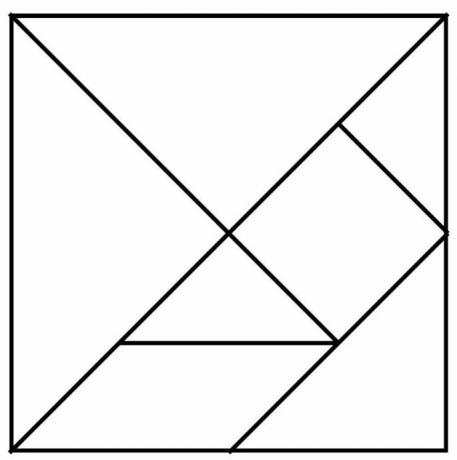
Paulo wants to put on his shelf three of his 10 school books, all different from each other, how many ways can he organize these books?
Note that, in this case, the order is important, but there are no repetitions, as it is a simple arrangement. To find the number of possible groupings, we have to:
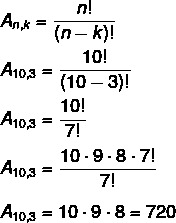
To learn more about this other form of grouping used in combinatorial analysis, read the text: THEsimple arrangement.
Exercises solved:
Question 1 - (Enem) A bank asked its customers to create a personal six-digit password, consisting only of numbers from 0 to 9, to access the checking account via the internet. However, a specialist in electronic security systems recommended that the bank's management re-register its users, requesting to each one of them, the creation of a new password with six digits, now allowing the use of the 26 letters of the alphabet, besides the digits from 0 to 9. In this new system, each capital letter was considered distinct from its lowercase version. In addition, the use of other types of characters was prohibited.
One way to evaluate a change in the password system is to check the improvement coefficient, which is the reason for the new number of password possibilities in relation to the old one. The recommended change improvement coefficient is:
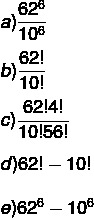
Resolution
Alternative A
The old password is an array with repetition, as it can be made up of all numbers, so it is an array of 10 elements taken every six.
AIR10,6 = 106
The new password can consist of 10 digits and also capital letters (26 letters) and lowercase (26 letters), so the password has, for each digit, a total of 10 + 26 + 26 = 62 possibilities. Since there are six digits, we will calculate the arrangement with repetition of 62 elements taken every six.
AIR62,6 = 626
THE reason of the new number of password possibilities compared to the old one is equal to 626/106.
Question 2 - (Enem 2017) A company will build its website and hopes to attract an audience of approximately one million customers. To access this page, you will need a password with a format to be defined by the company. There are five format options offered by the programmer, described in the table, where “L” and “D” represent, respectively, capital letter and digit.
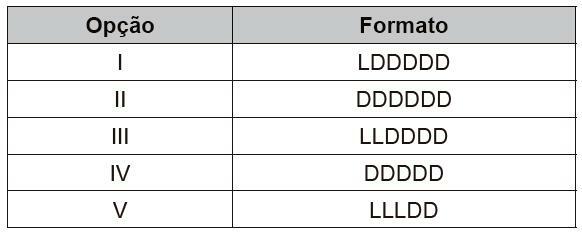
The alphabet letters, among the 26 possible, as well as the digits, among the 10 possible, can be repeated in any of the options.
The company wants to choose a format option whose number of possible distinct passwords is greater than expected number of customers, but that this number does not exceed twice the expected number of customers.
Resolution
Alternative E
By calculating each of the possibilities, we want to find the password that has more than a million possibilities and less than two million possibilities.
I → LDDDDD
26 ·105 is greater than two million, so it does not satisfy the company's request.
II → DDDDDD
106 is equal to one million, so it doesn't satisfy the company's request.
III → LLDDDD
26² · 104 is greater than two million, so it does not satisfy the company's request.
IV → DDDDD
105 it's less than a million, so it doesn't satisfy the company's request.
V → LLLDD
26³ ·10² is between one million and two million, so this password template is ideal.
Image credit
[1] Rafael Berlandi / Shutterstock
By Raul Rodrigues de Oliveira
Maths teacher