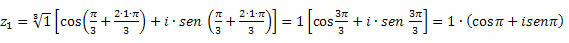An equation is exponential when the unknown (unknown value) is in the exponent of a power. Thus, a mathematical sentence that involves equality between two terms, where the unknown appears in at least one exponent, is called an exponential equation.
A power is the result of the product of its base by itself, as many times as determined by the exponent.
In an exponential equation we determine how many factors are multiplied, that is, how many times the base is multiplied, in order to obtain a certain result.
Definition of exponential equation:
Where:
b is the base;
x is the exponent (unknown);
a is the power.
On what It is
.
Example of an exponential equation:
The unknown variable is in the exponent. We must determine how many times 2 will multiply to result in 8. Like 2. 2. 2 = 8, x = 3, as 2 must be multiplied three times to obtain 8 as a result.
How to solve exponential equations
Exponential equations can be written in various ways and to solve them, we will use equal powers with equal bases, which must also have the same exponents.
As the exponential function is injective, we have:
This means that two powers with the same base will be equal if and only if their exponents are also equal.
Thus, one strategy for solving exponential equations is equalize the bases of powers. Once the bases are the same, we can eliminate them and compare the exponents.
To equalize the bases of powers in an exponential equation, we use mathematical tools such as factorization and potentiation properties.
Examples of solving exponential equations
Example 1
It is an exponential equation, as the sentence involves an equality (equation) and the unknown variable x is in the exponent (exponential).
To determine the value of the unknown x, we equate the bases of the powers, using the factorization of 64.
64 = 2. 2. 2. 2. 2. 2 or
Substituting into the equation:
We disregard the bases, leaving only equality between the exponents.
x = 6
Thus, x = 6 is the result of the equation.
Example 2
We equate the bases using factorization.
- 9 = 3. 3 =
- 81 = 3. 3. 3. 3 =
Substituting into the equation:
Using the power property of a power, we multiply the exponents on the left side.
With the bases equal, we can discard them and equal the exponents.
Thus, x = 1 is the result of the equation.
Example 3
We transform the base 0.75 into a centesimal fraction.
We simplify the centesimal fraction.
We factor 9 and 16.
Equating the bases, we have x = 2.
x = 2
Example 4
We transform the root into a power.
We factor the power bases.
By multiplying the exponents, we equal the bases.
Therefore, we have to:
Example 5
Factoring 25
We rewrite the power of 5² to the x. Changing the order of exponents.
We use an auxiliary variable, which we will call y.
(keep this equation, we will use it later).
Substituting into the previous equation.
Solving the quadratic equation, we have:
The solution set for the quadratic equation is {1, 5}, however, this is not the solution to the exponential equation. We must go back to the variable x, using
For y = 1:
For y = 5:
The solution set for the exponential equation is S={0, 1}.
Learn more about powers:
- Potentiation
- Potentiation: how to calculate, examples and exercises
- Exponential Function
For exercises:
- 17 strength training exercises with commented template
- Exponential function exercises (solved and commented)
ASTH, Rafael. Exponential equation.All Matter, [n.d.]. Available in: https://www.todamateria.com.br/equacao-exponencial/. Access at:
See too
- 27 Basic Mathematics exercises
- 17 strength training exercises with commented template
- Radiciation Exercises
- Second degree equation
- Exponential Function - Exercises
- Scheduling of Linear Systems
- Simple and Compound Interest
- 11 exercises on matrix multiplication