THE Trigonometry is one of the most important contents studied within the Geometry. Exercises involving this area are very frequent in vestibular and Enem. So it's good to know the mistakes most students make and know how to avoid them on these exams.
1st – Mistake the trigonometric ratios
At trigonometric ratios constitute the most basic part of the Trigonometry, however, there are still people who make mistakes by inverting some of its elements, or replacing values incorrectly. At reasonstrigonometric they are:
Senα = opposite side
hypotenuse
Cosα = adjacent catet
hypotenuse
Tgα = opposite side
adjacent catet
In this case, the most frequent thing is to correctly interpret the exercise, but substitute the measure of the adjacent leg in the sine or the measure of the opposite leg in the cosine. It is also very common to appear exercises that can only be solved by means of a tangent, and any of the others can be used. reasonstrigonometric, which hinders the correct resolution of the issue.
Tips
There are some important troubleshooting tips that include one of these reasonstrigonometric:
1 - The only one reasontrigonometric that doesn't involve the hypotenuse and the tangent. Therefore, to find the measure of one of the sides of a right triangle, knowing only the measure of one of the acute angles and of the other side, it is necessary to use a tangent.
2 – If the value of hypotenuse is given, there will be cases where you can choose any reasontrigonometric to solve the problem. There will also be those exercises in which only one of them can be used.
3 – Note that only two sides and one angle of triangle can be used in reasonstrigonometric. If one of these sides is the hypotenuse and the other does not touch the angle in question, the ratio is sine. If one side is the hypotenuse and the other touches the angle in question, the reason will be cosine.
2nd – Mistake the trigonometric ratio values table
The table of values of reasonstrigonometric is very simple, and it contains the values of the sine, cosine and tangent of notable angles, that is, angles of 30°, 45° and 60°.
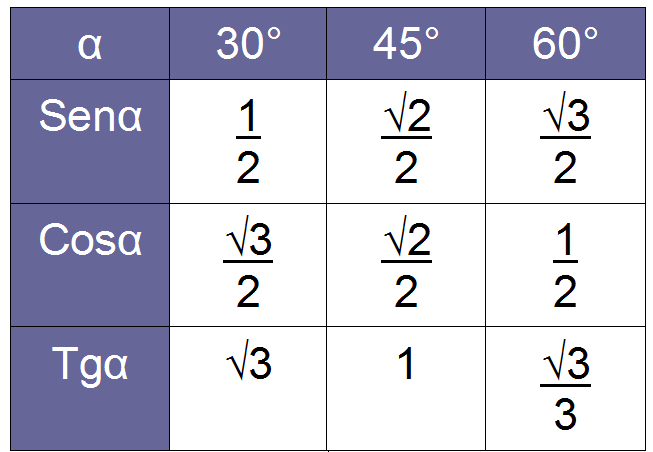
This table must be consulted every time it is necessary to calculate sine, cosine and/or tangent from an angle, as it provides one of the members of the proportion that makes these calculations possible.
In the following triangle, for example, the value of x can be given by the sine of the 45° angle.

The value of x must be calculated using the reasonsine, by replacing the values of the opposite leg and hypotenuse:
sen45° = x
10√2
Now we replace sen45° by its value, which is given in the table.
√2 = x
2 10√2
2x = 10√2∙√2
2x = 10∙2
x = 10 cm.
The most common mistake made regarding this table is related to confusing its values. If, instead of √2/2, we had placed √3/2, which is the sine of 60° and not 45°, the result found would be incorrect.
It is very common for the values of sen60° to be confused with cos60°, sen30° with cos30° and, especially, tg30° with tg60°. Therefore, it is important to know this table well, since these values are not usually given in entrance exams and in Enem.
3rd – Lack of mastery in Basic Mathematics
The vast majority of those preparing for exams such as Enem, entrance exams and competitions know well almost all the rules, relationships, properties and definitions required in these tests. In general, these people make mistakes in the questions, or fail to resolve them, due to deficiencies in the bases, such as lack of mastery of basic Mathematics.
Miscalculations due to lack of attention are extremely common. The most frequent are related to signs and operationsmathsbasics. However, other knowledge is also part of this content, such as the basic definitions of figuresgeometric, of other operations and even the knowledge of some properties that involve them.
So, as rare as exercises that ask “what is a square?”, “what are the main characteristics of isosceles triangles?”, “how to determine the measurement of the diagonal of a parallelogram?" etc., it is extremely common that the exercises make indirect use of these knowledge, so that it would only be possible to resolve them based on the responses of these questions.
To the Trigonometry, in addition, it is extremely important to know how to solve equations of the first It's from high school, simplify radicals and perform divisions and multiplications.
4th – Misinterpretation of the problem
In addition to knowing the properties that can be used in each situation and the rules of Mathbasic and of the Trigonometry, to solve problems, it is also necessary to have a good command of text interpretation. These statements are from Mathematics, but involve reading and interpretation, especially in Enem, which usually presents its questions in context.
What would be, for example, the perimeter of the triangle below?
a) 20 cm
b) 20(2 + √2)
c) 60 cm
d) 20 + √2 cm
e) √2 cm

Calculating the value of x is easy. We can use sine or cosine, as the measure of the hypotenuse is relevant for the calculation.
sen45° = x
20√2
√2 = x
2 20√2
2x = 20∙√2∙√2
2x = 20∙2
x = 20 cm.
At the end of this exercise we are tempted to mark alternative A, however, remember that the exercise asked for the perimeter of the triangle and not the value of x. As the perimeter of the polygon is the sum of the measurements of the sides, we will have:
P = 20 + 20 + 20√2
P = 40 + 20√2
or
P = 20(2 + √2) cm.
Template: Alternative B
By Luiz Paulo Moreira
Graduated in Mathematics
Source: Brazil School - https://brasilescola.uol.com.br/matematica/os-4-erros-mais-cometidos-na-trigonometria-basica.htm