Division of polynomials has different resolution methods. We will present three methods for this division: the Descartes method (coefficients to be determined), the key method and the practical Briot-Ruffini device.
read more: Polynomial equation: form and how to solve
polynomial division
When dividing a polynomial P (x) by a non-zero polynomial D (x), where the degree of P is greater than D (P > D), means that we must find a polynomial Q (x) and R (x), so that:
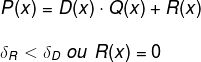
Note that this process is equivalent to writing:
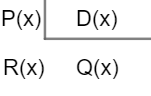
P (x) → dividend
D (x) → divisor
Q (x) → quotient
R (x) → remainder
From the properties of the potentiation, we have to quotient degree is equal to the difference between the dividend and divisor degrees.
Q = P - D
Also, when the remainder of the division between P(x) and D(x) is equal to zero, we say that P(x) is divisible by D(x).

Polynomial Division Rules
Method of coefficients to be determined — method of discards
To perform the division between polynomials P (x) and D (x), with degree of P greater than degree of D, we follow the steps:
Step 1 - Determine the degree of the quotient polynomial Q (x);
Step 2 - Take as much degree as possible for the remainder of the division R(X) (Remember: R(x) = 0 or R < D);
Step 3 - Write the Q and R polynomials with literal coefficients, so that P(x) = D(x) · Q(x) + R(x).
Example
Knowing that P (x) = 4x3 – x2 + 2 and that D (x) = x2 + 1, determine the quotient polynomial and the rest.
The degree of the quotient is 1 because:
Q =P - D
Q =3 – 2
Q = 1
So in the polynomial Q(x) = a·x +b, the remainder R(x) is a polynomial whose highest degree can be 1, hence: R(x) = c ·x +d. Replacing the data in the condition of step 3, we have:
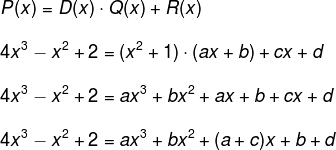
Comparing the coefficients of the polynomials, we have:
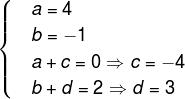
Hence, the polynomial Q (x) = 4x-1 and R (x) = -4x + 3.
c methodhave
It consists of performing the division between polynomials following the same idea of dividing two numbers, the call division algorithm. See the following example.
Again let's consider the polynomials P(x) = 4x3 – x2 + 2 and D (x) = x2 +1, and now we're going to split them using the key method.
Step 1 - Complete the dividend polynomial with null coefficients, if necessary.
P(x) = 4x3 – x2 + 0x + 2
Step 2 - Divide the first term of the dividend by the first term of the divisor and then multiply the quotient by every divisor. Look:

Step 3 - Divide the remainder from step 2 by the quotient and repeat this process until the degree of the remainder is less than the degree of the quotient.
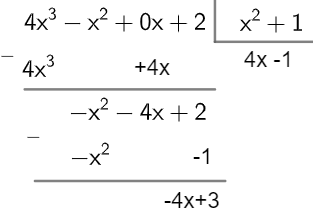
Hence, Q (x) = 4x-1 and R (x) = -4x +3.
Also access: Addition, subtraction and multiplication of polynomials
Briot's practical deviceRuffini
used for divide polynomials by binomials.
Let's consider the polynomials: P(x) = 4x3 + 3 and D (x) = 2x + 1.
This method consists of drawing two segments, one horizontal and one vertical, and on these segments we put the coefficient of the dividend and the root of the divisor polynomial, in addition, the first is repeated coefficient. Look:

Note that the smallest mean is the root of the divisor and that the first coefficient has been divided.
Now, we must multiply the root of the divisor by the repeated term and add it to the next, see:

The last number found in the practical device is the remainder, and the rest are the coefficients of the quotient polynomial. We must divide these numbers by the first coefficient of the divisor, in this case by 2. Thus:

To learn more about this method of dividing polynomials, go to: division of polynomials using the Briot-Ruffini device.
solved exercises
Question 1 (UFMG) The polynomial P (x) = 3x5 - 3x4 -2x3 + mx2 is divisible by D (x) = 3x2 - 2x. The value of m is:
Solution
Since the polynomial P is divisible by D, then we can apply the division algorithm. Thus,
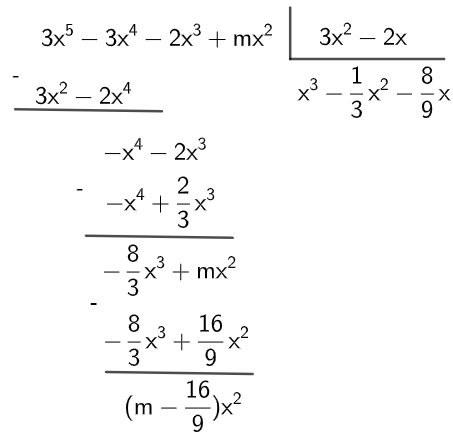
Since it was given that polynomials are divisible, then the remainder is equal to zero. Soon,

by Robson Luiz
Maths teacher
Source: Brazil School - https://brasilescola.uol.com.br/matematica/divisao-de-polinomios.htm

