THE inverse function, as the name suggests, is the function f(x)-1, which does exactly the inverse of the function f(x). For a function to support an inverse, it must be bijector, that is, injector and surjector at the same time. The formation law of an inverse function does the opposite of what the function f(x) does.
For example, if the function takes a value from domain and adds 2, the inverse function, instead of adding, subtracts 2. find the inverse function formation law it is not always an easy task, as it is necessary to invert the unknowns x and y, as well as to isolate y in the new equation.
Read too:Function - everything you need to know to master the subject
When does a function support inverse?
A role is invertible, that is, it has an inverse function, if, and only if, it is bijector. It's important to remember what a bijector function, which is a function injector, that is, every element of the image has a single domain correspondent. This means that different elements in set A need to be associated with different elements in the set B, that is, there cannot be two or more elements of set A that have the same corresponding in the set B.
A role is surjective if the image is equal to the counterdomain, that is, there is no element in set B that does not have an element in set A associated with it.
Let the function f: A → B, where A is domain and B is counterdomain, the inverse function of f will be the function described by f-1 : B→ A, that is, the domain and the counterdomain are inverted.
Example:
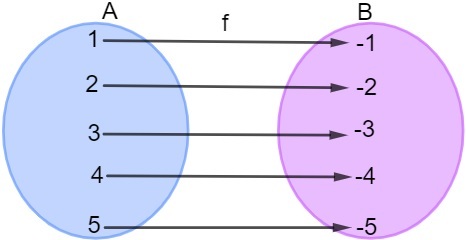
The function f: A → B is bijective, as it is injective (after all, distinct elements in A are associated with distinct elements in B) and it is also surjective, as there is no element left in set B, that is, the counterdomain is the same as the set Image.
Therefore, this function is invertible, and its inverse is:

How is the inverse function formation law determined?
To find the inverse function formation law, we need reverse the unknowns, that is, replacing x by y and y by x, and then isolating the unknown y. For this, it is important that the function is invertible, that is, bijector.
→ Example 1
Find the law of formation of the inverse function of f (x) = x + 5.
Resolution:
We know that f(x) = y, so y = x + 5. Performing the inversion of x and y, we will find the following equation:
x = y + 5
Now, let's isolate the y:
– 5 + x = y
y = x – 5
Clearly, if f(x) adds 5 to the value of x, then its inverse f(x) - 1 will do the reverse, that is, x minus 5.
→ Example 2
Given the function whose formation law is f (x) = 2x – 3, what will be the formation law of its inverse?
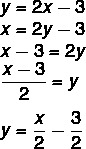
→ Example 3
Calculate the formation law of the inverse of the function y = 2x.
Resolution:
y = 2x
Changing x for y:
x = 2y
applying logarithm on both sides:
log2x = log22y
log2x = ylog22
log2x = y · 1
log2x = y
y = log2x
Read too: Differences between function and equation
Do not stop now... There's more after the advertising ;)
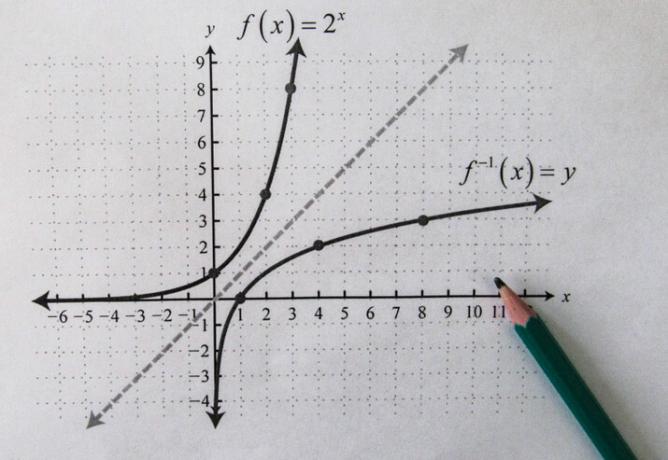
Inverse Function Graph
The graph of the inverse function f -1 it will always be symmetrical to the graph of the function f in relation to the line y = x, which allows to analyze the behavior of these functions, although we cannot describe the inverse function formation law in some cases, due to its complexity.

Read too: How to graph a function?
solved exercises
1) If f-1 is the inverse function of f, which goes from R to R, whose formation law f (x) = 2x – 10, the numerical value of f -1(2) é:
to 1
b) 3
c) 6
d) -4
e) -6
Resolution:
→ 1st step: find the inverse of f.

→ 2nd step: replace 2 in place of x in f -1(x).

Alternative C.
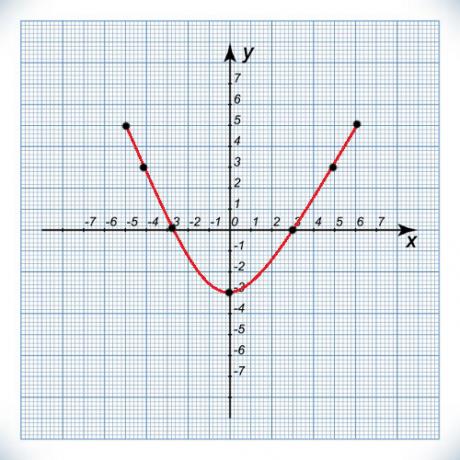
2) Let f: A → B be a function whose formation law is f (x) = x² + 1, where A {-2, -1, 0, 1, 2} and B = {1,2,5}, it is correct to say that:
a) the function is invertible, as it is bijector.
b) the function is not invertible, as it is not injecting.
c) the function is not invertible, as it is not surjective
d) the function is not invertible, as it is neither surjective nor injecting.
e) the function is not invertible, as it is bijector.
Resolution:
For the function to be invertible, it needs to be bijective, that is, surjective and injecting. First let's analyze if it is surjective.
For the function to be surjective, all elements of B must have a counterpart in A. To know this, let's calculate each of its numerical values.
f (-2) = (-2)² +1 = 4+1=5
f (-1) = (-1)² +1 = 1+1=2
f (0) = 0² +1 = 0+1=1
f(1) = 1² +1 = 1+1=2
f(2) = 2² +1 = 4+1=5
Note that all elements of B {1,2,5} have a corresponding in A, which makes the function surjective.
For this function to be injecting, elements distinct from A must have distinct images in B, which does not happen. Note that f(-2) = f (2) and also that f(-1) = f (1), which makes the function don't be injecting. As it is not an injector, it is also not invertible; therefore, alternative b.
By Raul Rodrigues de Oliveira
Maths teacher