We call a polygon a figure formed by straight line segments that delimit a region. Polygons must be closed figures. Watch:
Polygons have the following elements: vertices, sides, inside angles, outside angles and diagonals. From the elements mentioned, we will study the meaning of diagonals and how to calculate the number of diagonals of any polygon.
we call by diagonal the line segment that joins one vertex to another. The number of diagonals in a polygon is proportional to the number of sides.
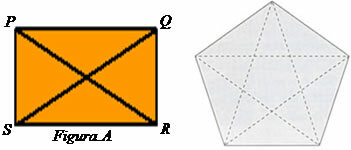
Note that in figure A we have four vertices, so we draw four diagonals, each starting at a vertex. But notice that the PR diagonal is the same RP, and the SQ diagonal is the same QS, so we'll always divide the number of diagonals by 2. For calculations involving the number of diagonals, we use the following formula:
Do not stop now... There's more after the advertising ;)
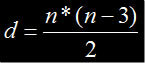
The formula n indicates the number of sides and n – 3 determines the number of diagonals that start from a single vertex and the division by two eliminates the duplication of diagonals occurring in a polygon.
Example
Determine the number of diagonals in a polygon with:
a) 8 sides (octagon)
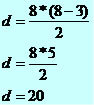
The octagon has 20 diagonals.
b) 12 sides (dodecagon)

The dodecagon has 54 diagonals.
c) 20 sides (icosagon)
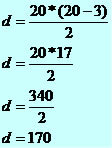
The number of diagonals of an icosagon is equal to 170.
d) 3 sides (triangle)

The triangle is the only polygon that does not have diagonals.
by Mark Noah
Graduated in Mathematics
Brazil School Team
plane geometry - Math - Brazil School
Would you like to reference this text in a school or academic work? Look:
SILVA, Marcos Noé Pedro da. "Number of Diagonals of a Convex Polygon"; Brazil School. Available in: https://brasilescola.uol.com.br/matematica/numero-diagonais-um-poligono-convexo.htm. Accessed on June 27, 2021.



