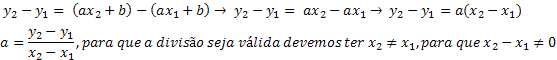The concepts and applications of trigonometric ratios emerged from studies carried out on the right triangle. By relating the opposite side, the adjacent side and the hypotenuse, we determine the relationships given by sine, cosine and tangent. Watch:

The study of these relationships is also associated with the angles of the trigonometric circle. In the circle, we obtain the ratios sine, cosine and tangent, as well as their reciprocal (inverse relationships) cosecant, secant and cotangent.
Do not stop now... There's more after the advertising ;)

Because the cosecant, secant and cotangent relationships are inverse, their representations can take the following notations:

The relationships are presented by Mathematics through the following abbreviations:
Sine: sen
Cosine: waistband
Tangent: tg
Cosecant: cossec
Secant: sec
Cotangent: cotg
by Mark Noah
Graduated in Mathematics
Would you like to reference this text in a school or academic work? Look:
SILVA, Marcos Noé Pedro da. "The Reciprocal Reasons of the Sine, the Cosine and the Tangent";
Brazil School. Available in: https://brasilescola.uol.com.br/matematica/as-razoes-reciprocas-seno-coseno-tangente.htm. Accessed on June 27, 2021.