For what polygons be enrolled or circumscribed, there needs to be a circumference, as it will be the basis for defining these processes. It is possible to recognize a circumscribed polygon easily, but it is not always simple to construct this type of figure. Before discussing this construction, it is worth commenting on the definition of polygon, polygon regular and circumscribed polygon.
Polygon, regular polygon and inscribed polygon
One polygon is a closed line formed only by straight segments that do not intersect. To be classified as regular, a polygon must have all the congruent sides and all yours angles internal with equal measures. Finally, it will be considered circumscribed at circumference c, if all its sides are tangent to it. Note that the inscribed polygon is within the circumference, and the circumscribed polygon is outside her.
The following image refers to a polygonregularcircumscribed on circumference c.
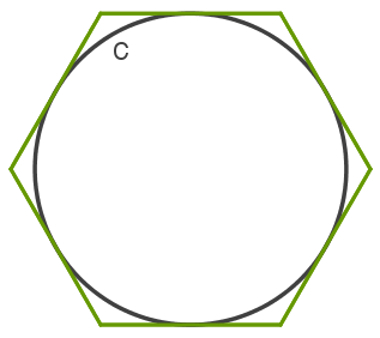
Construction of the regular circumscribed polygon
The work of building a
polygonregularcircumscribed is in positioning the circumference so that all sides of this polygon are tangents to her. This work can be minimized by following a sequence of steps, presented below:Do not stop now... There's more after the advertising ;)
1st – The center of the polygon, because when this figure is regular, its center is also the center of the circumference. To do this, trace the bisectors of this polygon according to what is done in the image below. As it is regular, these lines are at its center:

For this step, remember that the bisector is a straight perpendicular to one side of a polygon, dividing it into two equal parts.
2º – Suppose that one of these bisectors has found one of the sides of the polygon at point P. The OP segment will be the radius of the circumference enrolled in polygonregular. Use a compass to build this circle according to what is represented in the following image:
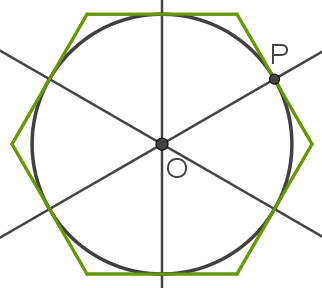
Note that the radius of the circumferenceenrolled in the regular polygon it is equal to its apothema. In the case where the circle is circumscribed, that is, if the polygon is inscribed, the radius of the circle is equal to the radius of the polygon.
By Luiz Paulo Moreira
Graduated in Mathematics
Would you like to reference this text in a school or academic work? Look:
SILVA, Luiz Paulo Moreira. "Construction of circumscribed polygons"; Brazil School. Available in: https://brasilescola.uol.com.br/matematica/construcao-poligonos-circunscritos.htm. Accessed on June 28, 2021.
slope, perpendicular lines, slope of perpendicular lines, condition of existence of perpendicular lines, tangent, inclination angle.


