For a better understanding and learning of Mathematics and Geometry, we need to highlight the knowledge of the axioms related to such sciences. Axioms are also known as postulates and are propositions accepted without proof.
An important and very useful axiom in geometry involves the study of the point, the line and the plane.
Through a single point, infinite straight lines pass.
A single straight line passes through two distinct points A and B.
To determine a plan we need at least three points.
If two distinct points on a line belong to a plane, then all points on that line belong to the plane. 
There are infinite points in and out of a plane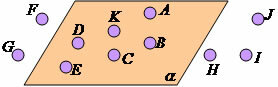
Relative positions of two lines
Two distinct lines have at most one common point.
competitors
They have only one point in common.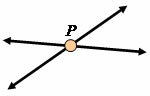
parallel
They have no common ground.
Postulates of Euclid
Two equal things added to a third are equal to each other.
If we add equal portions to equal amounts, the sums will remain the same.
If the same amounts are subtracted from the same amounts, the remainders will remain the same.
Situations that coincide are the same with each other.
The whole is greater than the parts.
by Mark Noah
Graduated in Mathematics
Brazil School Team
Spatial Geometry - Math - Brazil School

