Numerical sets are collections of numbers that have similar characteristics. They were born as a result of the needs of humanity in a certain historical period. See what they are!
Set of Natural Numbers
The set of Natural Numbers it was the first that was heard. It was born from the simple need to do counts, so its elements are just whole numbers and not negative.
Represented by N, the set of natural numbers has the following elements:
N = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, …}
Set of Integers
The set of whole numbers it is an extension of the set of natural numbers. It is formed by joining the set of natural numbers with negative numbers. In other words, the set of integers, represented by Z, has the following elements:
Z = {…, – 4, – 3, – 2, – 1, 0, 1, 2, 3, 4, …}
Set of Rational Numbers
The set of rational numbers born of the need to divide quantities. So this is the set of numbers that can be written as a fraction. Represented by Q, the set of rational numbers has the following elements:
Q = {x ∈ Q: x = a/b, a ∈ Z and b ∈ N}
The above definition is read as follows: x belongs to the rationals, such that x is equal to The divided by B, with The belonging to the integers and B belonging to the naturals.
In other words, if it's a fraction or a number that can be written as a fraction, then it's a rational number.
The numbers that can be written as a fraction are:
1 – All whole numbers;
2 – Finite decimals;
3 – Periodic tithes.
Finite decimals are those that have a finite number of decimal places. Watch:
1,1
2,32
4,45
Periodic decimals are infinite decimals, but they repeat the final sequence of their decimal places. Watch:
2,333333...
4,45454545...
6,758975897589...
Set of Irrational Numbers
the definition of irrational numbers depends on the definition of rational numbers. Therefore, all numbers that do not belong to the set of rationals belong to the set of irrational numbers.
In this way, either a number is rational or it is irrational. There is no possibility for a number to belong to these two sets simultaneously. In this way, the set of irrational numbers is complementary to the set of rational numbers within the universe of real numbers.
Another way to define the set of irrational numbers is as follows: The irrational numbers are those that no can be written in fraction form. Are they:
1 - Infinite decimals
2 – Roots not exact
Infinite decimals are numbers that have infinite decimal places and are not periodic tithes. For example:
Do not stop now... There's more after the advertising ;)
0,12345678910111213...
π
√2
Set of Real Numbers
The set of real numbers is formed by all the numbers mentioned above. Its definition is given by the union between the set of rational numbers and the set of irrational numbers. Represented by R, this set can be mathematically written as follows:
R = Q U I = {Q + I}
I is the set of irrational numbers. In this way, all the numbers mentioned above are also real numbers.
Complex Number Set
The set of complex numbers born from the need to find non-real roots of equations of degree greater than or equal to 2. When trying to solve the x equation2 + 2x + 10 = 0, for example, through Bhaskara's formula, we will have:
x2 + 2x + 10 = 0
a = 1, b = 2 and c = 10
? = 22 – 4·1·10
? = 4 – 40
? = – 36
What second degree equations do they have? < 0 have no real roots. To find their roots, the set of complex numbers was created, so that √–36 = √36·(–1) = 6·√– 1 = 6i.
The elements of the set of complex numbers, represented by C, are defined as follows:
z is a complex number if z = a + bi, where a and b are real numbers and i = √– 1.
Relationship between numeric sets
Some numeric sets are subsets of others. Some of these relationships were highlighted throughout the text, however, all of them will be explained below:
1 – The set of natural numbers is a subset of the set of integers;
2 – The set of whole numbers is a subset of the set of rational numbers;
3 – The set of rational numbers is a subset of the set of real numbers;
4 – The set of irrational numbers is a subset of the set of real numbers;
5 – The set of irrational numbers and the set of rational numbers do not have any elements in common;
6 – The set of real numbers is a subset of the set of complex numbers.
Indirectly, it is possible to establish other relationships. It is possible to say, for example, that the set of natural numbers is a subset of the set of complex numbers.
It is also possible to make the opposite reading of the relationships mentioned above and the indirect relationships that can be built. To do so, it is enough to say, for example, that the set of integers contains the set of natural numbers.
Using set theory symbology, these relationships can be written as follows:
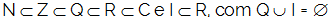
By Luiz Paulo Moreira
Graduated in Mathematics


