Unlike the geometric figures formed by him, the Score has no definition. This means that, in Geometry, a point is an undefined object used in defining other objects. Lines, for example, are sets of points. Although they look well defined, the lines also have no definition, as any set containing two or more points is considered straight.
On the other hand, in Analytical Geometry, the point is taken as a location. Any location can be represented by a point and, in addition, the “address” of that point is given by means of coordinates.
However, in analytic geometry, points are only able to indicate locations. Other objects are needed to indicate trajectory, direction, direction and intensity. In the case of these last three, the object chosen to represent them in the Cartesian plane is the vector.
→ What is a Vector?
Vectors, therefore, are objects that indicate direction, sense and intensity. They are usually represented by arrows, which start from the origin, and the coordinates of their last point are used.

In the image above, the vectors are represented in this way, that is, arrows whose coordinates correspond to their final point. Vector u has coordinates (2,2) and vector v has coordinates (4,2). Also, the arrow is used to indicate direction and direction, and its size indicates intensity.
→ Vector multiplication by a number
Given the vector v = (a, b), the product of the real number k by v is given by the expression:
k·v = k·(a, b) = (k·a, k·b)
In other words, to multiply a real number by a vector, you must multiply the real number by each of its coordinates.
Geometrically, multiplying a vector by a real number increases the vector's size linearly:

Note that, in the example above, vector u has coordinates (2.2), and vector u·k has coordinates (4.4). Solving the equation (4.4) = k (2.2), we can conclude that k = 2.
→ Adding vectors
Given two vectors u = (a, b) and v = (c, d), the sum between them will be obtained through the expression:
u + v = (a + c, b + d)
In other words, just add up the corresponding coordinates of each vector. This operation is expandable to sum of 3 or more vectors with 3 or more dimensions.
Geometrically, starting from the endpoint of vector u, a vector v' is drawn parallel to vector v. Starting from vector v, a vector u' is drawn parallel to vector u. These four vectors form a parallelogram. The vector u + v is the following diagonal of this parallelogram:
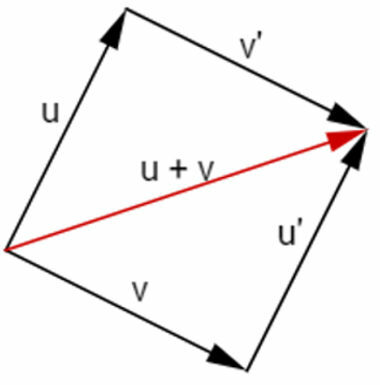
To subtract vectors, consider subtraction as the sum of one vector and the opposite of another. For example, to subtract vector v from vector u, write: u – v = u + (-v). The -v vector is the v vector, but with the coordinate signs reversed.
Looking closely, the operations "multiplying a vector by a number" and "adding vectors" make use of multiplication and addition operations on real numbers, but on each component of the vector. Therefore, for vectors, all properties of addition and multiplication of real numbers are valid, namely:
Given the vectors u, v and w and the real numbers k and l,
i) (u + v) + w = u + (v + w)
ii) u + v = v + u
iii) there is a vector 0 = (0.0) such that v + 0 = v
iv) There is a vector -v such that v + (-v) = 0
v) k (u + v) = ku + kv
vi) (k + l) v = kv + lv
vii) kl (v) = k (lv)
viii) 1v = v
→ Standard of a vector
The norm of a vector is the equivalent of the magnitude of a real number, that is, the distance between a vector and the point (0,0) or, depending on the frame of reference, the length of the vector.
The norm of the vector v = (a, b) is denoted by ||v|| and can be calculated using the expression:
||v|| = √(a2 + b2)
→ Internal product
Inner product is comparable to the product between vectors. Note that the product mentioned above is the product between a vector and a real number. Now, the “product” in question is between two vectors. However, one should not say “product between two vectors”, but rather “internal product between two vectors”. The inner product between the vectors v = (a, b) and u = (c, d) is denoted by
It is also customary to use the following notation:
Note that using the norm of the vector v = (a, b), we can relate the norm and the dot product.
||v|| = √(a2 + b2) = √(a·a + b·b) = √(
By Luiz Paulo Moreira
Graduated in Mathematics
Source: Brazil School - https://brasilescola.uol.com.br/matematica/operacoes-com-vetores-representacoes-geometricas.htm

