Round bodies: what are they, formulas, exercises

You round bodies, also called revolution solids, are objects of study of the spatial geometry. They are geometric solids that have rounded surfaces and they are very present in our daily lives, in objects such as a futsal ball, a birthday hat, a can of soda, etc.

Geometric solids considered round bodies are a sphere, cylinder and cone. Each of them has specific formulas for calculating its total area and volume.

Read too: Differences between flat and spatial figures

What are round bodies?

The cylinder, cone and sphere are round bodies.

We call round bodies the geometric solids that have their curved surfaces. They are also known as revolution solids, as they are constructed from the rotation of a flat figure.

Round bodies are very present in our daily lives, you can see them in a soda can, which has a cylindrical shape; in a soccer ball, which has a spherical shape; and also in a children's party hat or in the cones used by the traffic department have cone shapes.

What are round bodies?

• Cone

O cone

is a solid of revolution characterized by having a circle as its base. This geometric solid is built from the rotation of a triangle. A cone can be straight, when its height is in the center of the circumference that forms the base, or oblique, when its height does not coincide with the center of the base.

The cone is a solid of revolution.

To calculate the volume of a cone, it is necessary to know the radius of the base and its height.

As the base is always a circle, we can calculate the base area per

THE_B= πr²

O cone volume is the third of the multiplication between the base area and the height:

Knowing the plane of a cone, calculate the total area is to add the lateral area with the base area.

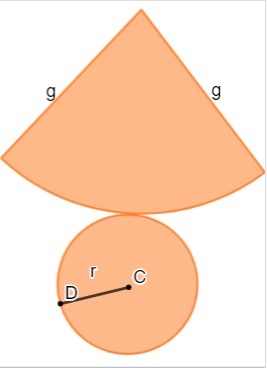
As the base of the cone is a circle, the base area is calculated from the formula:

THE_B= πr²

To calculate the side area, we need to know or find the value of the g generator of the cone. It can be calculated by Pythagorean theorem:

g² = r²+ h²

The lateral area, which is a circular sector, is calculated by:

THE_there=π·r·g

So the total cone area is the sum of A_B + A_there:

THE_T = πr (r + g)

See too: What is a Trunk Cone?

• Cylinder

The cylinder is characterized by having two circular bases of the same radius. As well as the cone, the cylinder can be classified as straight or oblique.

The cylinder is a round body.

To calculate the cylinder volume, we need to know its height value and the radius length of its base:

V = πr²·h

To calculate the total area, it is necessary to calculate the base area and the lateral area.

Cylinder Planning

THE_T = 2A_B + A_L

Since the base is a circle, then:

THE_B= πr²

The side area is a rectangle that has a base equal to the length of the circle and height h, so the side area is:

THE_L= 2πrh

Substituting the total area, we can calculate this area by the formula:

THE_T = 2πr (r + h)

• Ball

Unlike previous solids, the ballit does not have a circular base. It is built from the rotation of a semicircle.

A sphere is a round body constructed from the rotation of a circle.

To calculate the volume of the sphere, it is only necessary to know the radius:

The total area of ​​the sphere can be calculated by:

THE_T = 4πr²

Also access:What are the elements of the sphere?

Polyhedra and round bodies

Spatial geometry separates the geometric solids into two groups of equal importance, one of them is the round bodies we saw during the text, the others are the polyhedra, which are geometric solids whose faces are polygons.

They are polyhedra, for example, the parallelograms and the pyramids. Solids that do not fit into any of these sets are known as other solids.

Polyhedra

solved exercises

Question 1 - (UDESC 2015) A spherical ball is made up of 24 equal tracks, as shown in the figure.

Knowing that the volume of the ball is 2304 π cm³ then the surface area of ​​each band is:

A) 20π cm²

B)24π cm²

C)28π cm²

D)27π cm²

E)25π cm²

Resolution

Alternative B

Step 1: Find the radius of the sphere.

Knowing the volume, let's calculate the radius of the sphere.

2nd step: calculate the total area, knowing that the radius measures 12 cm.

3rd step: calculate the area of ​​a swath.

576π: 24 = 24π cm²

Question 2 - What is the ratio between the volume of a cone and the volume of a cylinder that have the same height?

A) 1/3

B) 2/3

C) 3/1

D) 3/2

E) 1/6

Resolution

Alternative A

By Raul Rodrigues de Oliveira
Maths teacher

Source: Brazil School - https://brasilescola.uol.com.br/matematica/corpos-redondos.htm