calculate the factorial of a number only makes sense when we are working with natural numbers. This operation is quite common in combinatorial analysis, facilitating the calculation of arrangements, permutations, combinations and other problems involving counting. The factorial is represented by the symbol “!”. We define it as n! (n factorial) to multiplication of n by all its predecessors until you reach 1. no! = n · (n – 1)· (n – 2) · … · 3 · 2 · 1.
Read too: Fundamental principle of counting - main concept of combinatorial analysis
What is factorial?
Factorial is a very important operation for the study and development of combinatorial analysis. In mathematics, the number followed by the exclamation symbol (!) is known as factorial, for example x! (x factorial).
We know as a factorial of a natural number The multiplying this number by its predecessors except zero, i.e:
no! = n · (n-1) · (n-2) … 3 · 2 · 1 |
It is noteworthy that, for this operation to make sense, n is a natural number, that is, we do not calculate factorial of a negative number, or even of a decimal number, or of fractions.

factorial calculation
To find the factorial of a number, just calculate the product. Also note that the factorial is an operation that, when increase the value of n, the result will also increase a lot.
Examples:
4! =4 · 3 · 2 · 1 = 24
5! = 5 · 4 · 3 · 2 · 1= 120
6! = 6 · 5 · 4 · 3 · 2 · 1 = 720
7! = 7· 6 · 5 · 4 · 3 · 2 · 1 = 5040
By definition, we have:
0! = 1
1! = 1
Do not stop now... There's more after the advertising ;)
Factorial operations
To solve factorial operations, it is important to be careful not to make any mistakes. When we are going to add, subtract or multiply two factorials, it is necessary to calculate each one of them separately. Only the division has specific ways to carry out simplifications. Don't make the mistake of performing the operation and keeping the factorial, either for addition and subtraction or for multiplication.
2! + 3! ≠ 5!
4! · 2! ≠ 12!
7! – 5! ≠ 2!
When solving any of these operations, we must calculate each of the factorials.
Examples:
a) 2! + 3! = (2 · 1) + (3 · 2 · 1) = 2 + 6 = 8
b) 4! · 2! = (4 · 3 · 2 · 1) · (2 · 1) = 24 · 2 = 48.
c) 7! - 5! =(7 · 6· 5· 4 · 3 · 2 · 1) - (5· 4 · 3 · 2 · 1) = 5040 – 120 = 4920.
See too: How to solve equation with factorial?
Factorial simplification
Divisions are quite recurrent. In formulas of combination, arrangement and permutation with repetition, we will always resort to simplification to solve problems involving factorial. For that, let's follow a few steps.
Example:

1st step: identify the largest of the factorials — in this case, it's 8! Now, analyzing the denominator, which is 5!, let's write the multiplication of 8 by its predecessors until we get to 5!.
The factorial of a number n, that is, n!, can be rewritten as the multiplication of n to k!. Thus,
no! = n·(n -1 ) · (n- 2 ) · … · k!, so let's rewrite 8! like the multiplication from 8 to 5!.
8! = 8 · 7 · 6 · 5!
So let's rewrite reason as:
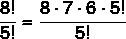
2nd step: after rewriting the reason, it is possible to simplify the numerator with the denominator, since 5! it is in both the numerator and the denominator. After simplification, just carry out the multiplication.

Example 2:
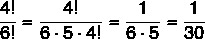
Combinatorial and Factor Analysis
When performing the further study in combinatorial analysis, the factorial of a number will always appear. The main groupings in combinatorial analysis, which are permutation, combination, and arrangement, use the factorial of a number in their formulas.
Permutation
THE permutation and the reordering all elements of a set. To calculate a permutation, we resort to factorial, as the permutation of n elements is calculated by:
Pno = n!
Example:
How many anagrams can we build with the name HEITOR?
This is a typical permutation problem. As there are 6 letters in the name, to calculate the number of possible anagrams, just calculate P6.
P6 = 6! = 6 · 5 · 4 · 3 · 2 · 1 = 720
Also access: Permutation with repeated elements: how to solve it?
Arrangements
Calculate arrangements it also requires mastering the factorial of a number. Arrangement, like permutation, is the formation of a reordering. The difference is, in the arrangement, we are reordering part of the set, that is, we want to know how many possible reorderings we can form by choosing a quantity k of one set with n elements.

Example:
In a company, there are 6 candidates to manage the institution, and two will be selected for the positions of director and deputy director. Knowing that they will be elected by vote, how many possible results are there?
In this case, we will calculate the arrangement of 6 taken from 2 by 2, as there are 6 candidates for two vacancies.

Combination
In the combination, as in the others, it is necessary to master the factorial of a number. We define as combination you subsets of a set. The difference is that, in the combination, there is no reordering, because the order is not important. So we are calculating how many subsets with k elements we can form in a set of n elements.
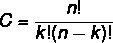
Example:
A committee of 3 students will be chosen to represent the class. Knowing that there are 5 candidates, how many commissions can be formed?
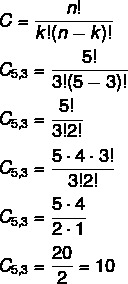
Read too: Arrangement or combination?
solved exercises
Question 1 - About the factorial of a number, judge the following statements.
I). 0! + 1! = 2
II). 5! - 3! = 2!
III) 2! · 4! = 8
A) Only I is true.
B) Only II is true.
C) Only III is true.
D) Only I and II are true.
E) Only II and II are true.
Resolution
Alternative A.
I) True.
0! = 1
1! = 1
0! + 1! = 1+1 = 2
II) False.
5! = 5 · 4 · 3 · 2 · 1= 120
3! = 3 · 2 · 1 = 6
5! – 3! = 120 – 6 = 114
III) False.
2! = 2 · 1
4! = 4 · 3 · 2 · 1= 24
Question 2 - (UFF) Is the product 20 · 18 · 16 ·14 … · 6 · 4 · 2 equivalent to?
A) 20:2
B) 2·10!
C) 20:210
D) 210· 10!
E) 20!: 10!
Resolution
Alternative D.
Looking at the product of all even numbers from 2 to 20, we know that:
20 = 2 · 10
18 = 2 · 9
16 = 2 · 8
14 = 2 · 7
12 = 2 · 6
10 = 2 · 5
8 = 2 · 4
6 = 2 · 3
4 = 2 · 2
2 = 2 · 1
So we can rewrite as 210 · 10 · 9 · … ·2 · 1 = 210 · 10!
By Raul Rodrigues de Oliveira
Maths teacher