Three-point alignment condition

When three points belong to the same straight, they are called aligned dots.

In the figure below, the points $\dpi{120} \mathrm{A}(x_1,y_1)$ , $\dpi{120} \mathrm{B}(x_2,y_2)$ and $\dpi{120} \mathrm{C}(x_3,y_3)$ they are aligned dots.

dots lined up

Three-point alignment condition

If points A, B and C are aligned, then triangles ABD and BCE are similar triangles, therefore, have proportional sides.

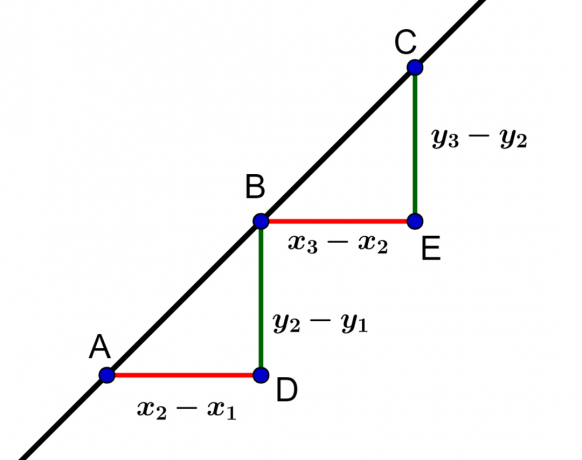
Alignment condition

$\dpi{120} \boldsymbol{\frac{x_2-x_1}{x_3-x_2} = \frac{y_2-y_1}{y_3-y_2}}$

So, the three-point alignment condition $\dpi{120} \mathrm{A}(x_1,y_1)$ , $\dpi{120} \mathrm{B}(x_2,y_2)$ and $\dpi{120} \mathrm{C}(x_3,y_3)$ any, is that the following equality is satisfied:

$\dpi{120} \boldsymbol{\frac{x_2-x_1}{x_3-x_2} = \frac{y_2-y_1}{y_3-y_2}}$

Examples:

Check that the dots are aligned:

a) (2, -1), (6, 1) and (8, 2)

We calculate the first side of the equality:

$\dpi{120} \frac{x_2-x_1}{x_3-x_2} = \frac{6 -2}{8-6} = \frac{4}{2}=2$

We calculate the second side of the equality:

Check out some free courses

Free Online Inclusive Education Course
Free Online Toy Library and Learning Course
Free Online Math Games Course in Early Childhood Education
Free Online Pedagogical Cultural Workshops Course

$\dpi{120} \frac{y_2-y_1}{y_3-y_2} = \frac{1-(-1)}{2-1} = \frac{2}{1}=2$

Since the results are equal (2 = 2), then the points are aligned.

b) (-2, 0), (4, 2) and (6, 3)

We calculate the first side of the equality:

$\dpi{120} \frac{x_2-x_1}{x_3-x_2} = \frac{4-(-2)}{6-4} = \frac{6}{2}=3$

We calculate the second side of the equality:

$\dpi{120} \frac{y_2-y_1}{y_3-y_2} = \frac{2-0}{3-2} =\frac{2}{1} =2$

Since the results are different (3 ≠ 2), then the points are not aligned.

instagram story viewer

Observation:

It is possible to show that if: $\dpi{120} \frac{x_2-x_1}{x_3-x_2} = \frac{y_2-y_1}{y_3-y_2}$

Then the matrix determinant of coordinates of the points is zero, that is:

$\dpi{120} \mathrm{\begin{vmatrix} x_1& y_1 & 1\\ x_2& y_2 & 1\\ x_3& y_3 & 1 \end{vmatrix} = 0}$

Therefore, another way to check whether three points are aligned is by solving the determinant.

You may also be interested:

straight equation
perpendicular lines
parallel lines
How to calculate the distance between two points
Differences between function and equation

The password has been sent to your email.

Attention! See what can and cannot in Enem 2020

Awaited by millions of students, the National High School Exam (And either) begins to be applied ...

History lesson plan

History lesson plan

Check out the lesson plan about the Monroe Doctrine that we've created for your 8th grade element...

1922 Modern Art Week

1922 Modern Art Week

Do you know what was the 1922 Modern Art Week and where was it performed? The Week of Modern Art ...