O right triangle gets this name because one of its angles has a measure of 90º, that is, it is a right angle. Being one of the most studied polygons in plane geometry, it was possible to see some relationships between the angles and also between the sides of this figure.
O Pythagorean theorem, for example, it was developed after the realization that there is a relationship between the measurements of the sides of the triangle. Thus, knowing the measurements of two sides of the triangle, it is possible to calculate the value of the third side. Pythagoras' theorem says that the sum of the square of the legs is always equal to the square of the hypotenuse.
In addition to the Pythagorean theorem, another important area developed through the studies of this triangle was the trigonometry, in which the ratios between the sides of the triangle, known as sine, cosine, and tangent, are developed. Through these reasons, it was noticed that there is a proportion between the measurements of the sides of right triangles that have equal angles.
Read too: What are the notable points of a triangle?
Right Triangle Features

The right triangle is a polygon that has three sidesand three angles, and one of these angles is straight, that is, it has 90º. The other two angles are acute, that is, less than 90º. The longest side, which is always opposite the 90° angle, is known as hypotenuse, and the other two are called peccaries.
The right triangle preserves all the known properties of the common triangle, such as the fact that The sum of internal angles be equal to 180º. As the sum is always 180º and one of its angles already has 90º, we can say that the other two angles are always complementary, that is, their sum is also equal to 90º.
a and b → breasts
c → hypotenuse
Perimeter of the right triangle
The perimeter of any polygon is the length of the sum of all its sides. So, to calculate the perimeter of the right triangle, just add its sides.
P = a + b + c
right triangle area
THE triangle area rectangle, as well as a triangle any, is half the product between the base and the height. What is special about the right triangle is that one of its legs coincides with its height, since they are perpendicular to each other, so to calculate the area, we multiply the legs and divide the result by two.

Example:
Calculate the perimeter and area of the right triangle below knowing that its sides are given in centimeters.

P = 8 + 15 + 17
P = 40 cm
Now let's calculate the area:
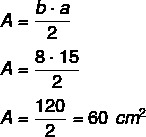
See too: Calculating the area of a triangle using angles
Pythagorean theorem
The best known theorem in mathematics is, without a doubt, the Pythagorean theorem. From this theorem, it was possible to see that the sides of a right triangle are related as follows: given any right triangle, the sum of the square of the legs is equal to the hypotenuse squared.
a² + b² = c²
a and b → breasts
c → hypotenuse
From this theorem, it is possible to find the value of either side of a right triangle, as long as the other two are known.
Example:
What is the value of the hypotenuse of the right triangle below knowing that its measurements are given in centimeters?
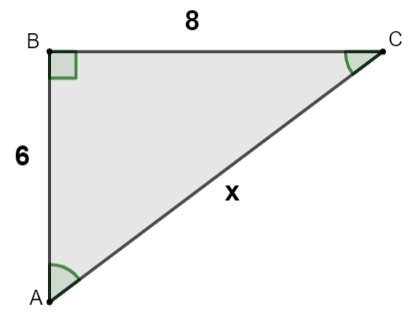
Applying the Pythagorean theorem, we have to:
6² + 8² = x²
36 + 64 = x²
100 = x²
x² = 100
x=√100
x = 10 cm
To learn more about this important relationship, read the text: TPythagoras' eorem.
Trigonometry in the right triangle
The name trigonometry already refers to its object of study:
- tri → three;
- gono → angle;
- metrics → metric or measure.
Thus, trigonometry is the area of Mathematics that studies the relationship between the measurements of the angles of the triangle and here we are going to stick to the right triangle. Trigonometry studies the ratio between the sides of the triangle according to its angle. With this, it was possible to develop important concepts, which are the reasons sine, cosine and tangent. It is worth mentioning that other trigonometric reasons were developed with the deepening of the study of trigonometry in the trigonometric circle.
Before understanding what each of these ratios are, it is important to understand what is an opposite side and what is an adjacent side at an angle of a triangle.
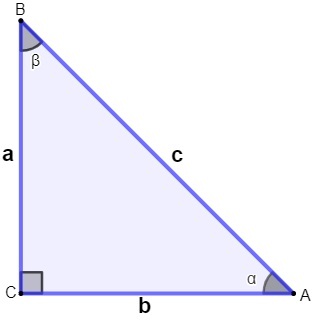
As we have seen, the hypotenuse is the side represented by segment AB, as it is always the longest side of the triangle and also the side facing 90º angle. The other sides are known as legs. Depending on the angle we take as reference, the side can be opposite or adjacent.
The peccary is known as the opposite when it faces the angle. The side opposite angle ꞵ, for example, is the side AC; on the other hand, the side that is opposite angle lado is the side BC.
O peccary is known as adjacent when he forms the angle near the hypotenuse. Note that angle ꞵ is between side BC and AB. Since AB is the hypotenuse of the right triangle, then AB is a leg adjacent to angle ꞵ. Using the same reasoning, you can see that the lado AC is the adjacent side of angle ɑ.
By understanding each side of the triangle, it is possible to understand the trigonometric ratios.

To apply trigonometric ratios, we must know the remarkable angles, that is, the angles of 30º, 45º and 60º. Most exam and entrance exam problems are linked to these angles, and it is therefore necessary to know the values of the reasons for each of them.
See the table with the sine, cosine and tangent values for the notable angles:

Knowing the value of the triangle's trigonometric ratios by means of a side and an angle, it is possible to find all sides of a right triangle from trigonometry.
Example:
Find the value of x.

To find the value of x, let's look at the angle that was given. Note that it is adjacent to the side we know the measure from, that is, AC is adjacent to the 30° angle. Then, we will apply the tangent ratio, which relates the adjacent side and the hypotenuse. Also, by looking at the table, we know that cosine of 30th is equal to √3/2.

Also access: 4 most common mistakes in basic trigonometry
solved exercises
Question 1 - (IFG) Theodolite is a precision instrument for measuring horizontal angles and vertical angles, used in construction work. A company was hired to paint a four-story building. To find out the total area to be painted, she needs to find the height of the building. One person positions the instrument at 1.65 meters high, finding an angle of 30°, as shown in the figure. Assuming that the theodolite is 13√3 meters away from the building, what is the height, in meters, of the building to be painted?

A) 11.65
B) 12.65
C) 13.65
D) 14.65
E) 15.65
Resolution
Alternative D.
Since we want to find the side opposite the 30° angle, knowing that the 13√3 distance, which is the distance from the theodolite to the building, is the side adjacent to the 30° angle, so we will use the tangent:
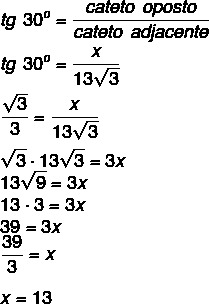
Now we will add 13 + 1.65 = 14.65 meters high.
Question 2 - To carry out planting on his property, a farmer divided his cultivable land in the rectangular shape in half, on its diagonal, forming two right triangles. In this division, half of the land will be fenced with wire, using 4 wires. Knowing that the dimensions of the land are 20 meters wide and 21 meters long, how much will be spent on wire?
A) 29 meters
B) 70 meters
C) 140 meters
D) 210 meters
E) 280 meters
Resolution
Alternative E.
First let's find the terrain diagonal, which is the hypotenuse of the right triangle. To make it easier, we will make a picture of the situation:
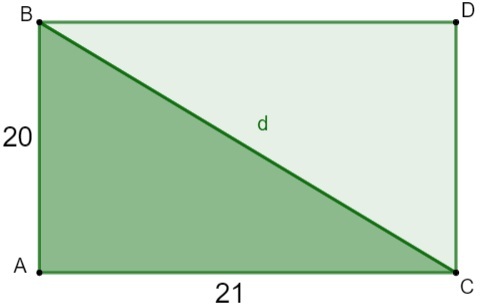
So, we have to:
d² = 20² + 21²
d² = 400 + 441
d² = 841
d = √841
d=29
To go around, we have to 29 + 20 + 21 = 70 meters, as will be 4 laps, 70 · 4 = 280 meters.
By Raul Rodrigues de Oliveira
Maths teacher
Source: Brazil School - https://brasilescola.uol.com.br/matematica/triangulo-retangulo.htm

