Two square difference is the 5th case of factorization. To better understand how and when to use it, we need to know that difference in mathematics is the same as subtraction and that squared is to square a number, letter, or terms.
Factoring by the difference of two squares can only be used when:
- We have an algebraic expression with two monomials (they are binomials).
- The two monomials are square.
- The operation between them is subtraction.
See some examples of algebraic expressions that follow this model:
• a2 - 1, the algebraic expression has only two monomials, both are squared and between them there is a subtraction operation.
• 1 - a2
3
• 4x2 - y2
►How to write the factored form of these algebraic expressions.
Given the 16x algebraic expression2 – 25, see the steps we must take to reach the factored form using the 5th factorization case.
The factored form will be (4x - 5) (4x + 5).
See some examples:
Example 1:
The algebraic expression x2 – 64 is an expression with two monomials and the square roots are respectively x and 8, so its factored form is (x – 8) (x + 8).
Example 2:
Given the algebraic expression 25x2 – 81, the root of terms 25x2 and 81 is respectively 5x and 9. So the factored form is (5x – 9) (5x + 9).
Example 3:
Given the 4x algebraic expression2 – 81y2, the root of 4x terms2 and 81y2 is respectively 2x and 9y. So the factored form is (2x – 9y) (2x + 9y).
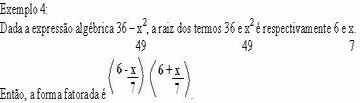
Do not stop now... There's more after the advertising ;)
by Danielle de Miranda
Mathematics Graduation
Brazil School Team
Algebraic Expression Factorization
Math - Brazil School
Would you like to reference this text in a school or academic work? Look:
RAMOS, Danielle de Miranda. "Difference of two squares"; Brazil School. Available in: https://brasilescola.uol.com.br/matematica/diferenca-dois-quadrados.htm. Accessed on June 28, 2021.