Gasideal is the one where the collisions between particles are perfectly elastic. Between his particles, there isn't any kind of interaction, like forces attractive or repulsive, moreover, these particles do not take up space.
According to the kinetic theory of gases, the thermodynamic state of an ideal gas is completely described by the variables of pressure, volume and temperature.
Lookalso: Calorimetry: mind map, formulas and solved exercises
ideal gas concept
Ideal gases are composed exclusively of particlesindimensionspunctual (of negligible size) that are in movementchaotic is on highvelocity. In this type of gas, the temperature and the speed of translation of the particles are proportional.
Since there is no interaction between the particles of an ideal gas, the internal energy of this gas is always equal to the sum of the kinetic energy of all the particles that constitute it.

Whatever the ideal gases are, they will always have the same
numberinparticles for the same volume. Their mass, in turn, will depend directly on your molar mass (measured in g/mol), in addition, 1 mole of ideal gas (about 6.0.1023 particles) will always occupy a volume equal to 22.4 l.You gasesreal, where there is occurrence of collisionsinelastic between particles, come very close to the behavior of ideal gases in low pressure and high temperature regimes. Coincidentally, under normal conditions of pressure and temperature on Earth (25 °C and 1 atm), most of the gases behave like ideal gases, and this facilitates the calculation of predictions about thermodynamic behavior their.
Some gases, like the water vapor, which is diluted in the atmospheric gas, can not be considered ideal gases but yes gasesreal. These gases have significant interactions between their particles, which can condense, causing them liquefy, if there is one temperature drop.
Characteristics of ideal gases
Check it out at abstract, some characteristics of ideal gases:
- In them only perfectly elastic collisions between particles occur;
- In them there are no interactions between particles;
- In them the particles have negligible dimensions;
- 1 mole of ideal gas occupies a volume of 22.4 l, regardless of what the gas is;
- Real gases behave like ideal gases when under low pressure and high temperature regimes;
- Most gases behave similarly to ideal gases.
ideal gas law
The study of gases developed by scholars Charlesboyle,JosephLouisgay-lussac and Robertboyle led to the emergence of three empirical laws, used to explain the behavior of ideal gases in regimes of temperature, pressure and volumeconstants, respectively.
Together these laws formed the necessary basis for the emergence of ideal gas law, which relates the initial thermodynamic state of a gas, defined by the quantities P1, T1 and V1, With your final thermodynamic state (P2, V2 and T2), after having suffered some gas transformation.
Check out the formula of the general gas law:
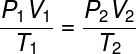
The general gas law states that the product gives pressure fur volumeofgas, divided by the thermodynamic temperature, in kelvin, is equal to a constant. This constant, in turn, is described by the clapeyron equation, watch:
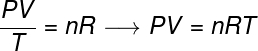
no – number of moles (mol)
R – universal constant of perfect gases (0.082 atm.l/mol. K or 8.31 J/mol. K)
In the formula, P is the pressure exerted by the gas, V is the volume occupied by this gas, and T is the temperature, measured in kelvin. the greatness no refers to the number of moles, while R is the universal constant of ideal gases, which is often measured in units of atm.l/mol. K or in J/mol. K, the latter being adopted by the SI.
Lookalso:What is solar wind and how does it affect Earth's atmosphere?
Internal energy of ideal gas
THE energyinternal of ideal gases can be calculated using the product between the constantinBoltzmann and the thermodynamic temperature, note:
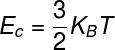
KB – Boltzmann constant (KB = 1,38.10-23 J/K)
From the previous relationship, which allows us to calculate the average kinetic energy from the particles of an ideal gas, we draw the following formula, which can be used to calculate what the mean square velocity of molecules of an ideal gas, for a given temperature T, note:
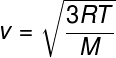
M – molar mass (g/mol)
This formula allows you to see that a additionattemperature of an ideal gas results in an increase in the mean square speed of the particles.
Know more:Find out what light is made of and what are its characteristics
Solved exercises on ideal gases
Question 1) Two moles of an ideal gas, and at a pressure of 1 atm, are found at a temperature of 227 °C. Calculate, in liters, the volume occupied by this gas.
Data: R = 0.082 atm.l/mol. K
a) 75 l
b) 82 l
c) 15 l
d) 27 l
e) 25 l
Template: Letter B
Resolution:
To calculate the volume of this gas, we will use the Clapeyron equation, however, before we do the calculation, it is necessary to transform the temperature of 227 °C into a kelvin. For this we add the factor 273 to this temperature, resulting in a temperature of 500 K.
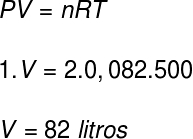
According to the resolution, the volume occupied by the gas is 82 liters.
Question 2) An ideal gas occupies a volume of 20 l, when it is subjected to a pressure of 3 atm, so that its temperature remains constant, while its volume is tripled. Calculate the final pressure of this gas after it has gone through this transformation.
a) 1 atm
b) 3 atm
c) 5 atm
d) 8 atm
e) 9 atm
Template: Letter a
Resolution:
To solve this exercise, we will use the general law of gases, note:

To make the calculation, it was necessary to assign a volume of 60 l to the gas, since its volume tripled during the transformation.
By Rafael Hellerbrock
Physics teacher

