THE simple combination is one of the groupings studied in combinatorial analysis. We know as a combination the count of all subsets of k elements that we can form from a set of no elements.
It is quite common to see situations where we use the combination, for example, to calculate all results possible in lottery games or poker games, and in other situations, such as in the study of probability and statistic.
Another very common grouping is the arrangement. What differentiates arrangement from combination is the fact that, in arrangement, the order of elements is important, and in combination, the order is not important. Therefore, we compare the combination with the choice of subsets.
Read too: Fundamental principle of counting - used to quantify the possibilities
What is simple combination?

In combinatorial analysis, the number of possible clusters is studied. Among these groupings, there is what is known as simple combination. The simple combination is nothing more than the
count of all subsets with k elements of a given set, for example: megassena, in which 6 numbers are drawn at random.In this case, you can see that the order in which these 6 numbers were chosen makes no difference, that is, the order doesn't matter, which makes this result a subset. This characteristic is fundamental to understand what a combination is and to differentiate it from the other groupings — in the combination, the order of the elements of the set does not matter.
simple combination formula
Problems involving combination are calculated by a formula. the combination of no elements taken from k in k é:

n → total elements in the set
k → total elements in subset
See too: Additive counting principle - union of elements of two or more sets
How to calculate a combination?
In the first place, it is important to know when a problem is a combination. To illustrate, find all possible combinations of the set {A, B, C, D} with two elements:
Listing combinations with two elements, they are: {A, B}, {A, C}, {A, D}, {B, C}, {B, D} and {C, D}. In this case, it is possible to see that there are 6 possible combinations, and it is also worth noting that the subsets {A, B} and {B, A} are equal, because, in the combination, the order is not important.
It turns out that it is not always possible to list all possible combinations or even it is not necessary, as the biggest interest is in the number of combinations and not in the listing of each one of them. For this, it is very practical to use the formula.
Example:
A school will draw three tickets, one for each student, among the top 10 in the math olympics. After completing the test and knowing the top 10 places, calculate the possible combinations for the draw result.
Note that, in the draw result, the order is not important, so we are working with a combination problem.
We will then calculate the combination of 10 elements taken from 3 out of 3. Substituting in the formula, we have to:

Now let's simplify the factorials. At this point, it is essential to master the calculation of the factorial of a number. Like 10! is greater than any of the factorials in the denominator, and, looking at the denominator, 7! is the biggest of them, let's do the multiplication of 10 by its predecessors until reaching 7!, so that it is possible to simplify.
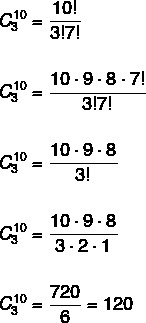
Pascal's triangle
One of the instruments widely used in combinatorial analysis, mainly to calculate a Newton's binomial, is Pascal's triangle. This triangle is constructed from the results of the combinations, another way to represent the combination of two numbers is as follows:
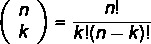
Pascal's triangle starts at row 0 and column 0, by combining 0 elements taken from 0 to 0. The lines are the same as no, and the columns equal to k, forming the following figure:

Substituting the values that result from the combinations:

Through the rows and columns of Pascal's triangle, it is possible to find the value of the combination we want. If necessary, we can find the terms of as many lines as needed. To learn more about this resolution method, read the text: Pascal's triangle.
Difference between arrangement and combination
Arrangement and combination are two equally important groupings studied in combinatorial analysis. It is essential to know the difference between each of these groups, that is, if we are going to calculate them by a arrangement or one combination.
It turns out that in the combination, when assembling the clusters, the order of the elements of the set is not important., ie {A, B} = {B, A}, but there are cases where order is important in the grouping, in this case we are working with an array.
At the arrangement, then, the order of the elements is different, that is, {A, B} ≠ {B, A}, an example of a very common arrangement would be to calculate how many different ways we can form the podium of a given competition between 10 people. Note that in this example, order is important, which makes it resolvable by the arrangement formula. In addition to the theoretical definition, the formulas are different, and the arrangement formula é:

solved exercises
question 1 – (Enem) Twelve teams signed up for an amateur soccer tournament. The opening game of the tournament was chosen as follows: first, 4 teams were drawn to make up Group A. Then, among the teams in Group A, 2 teams were drawn to play the opening game of the tournament, the first of which would play in their own field, and the second would be the visiting team. The total number of possible picks for Group A and the total number of picks for the teams in the opening game can be calculated using
A) a combination and an arrangement, respectively.
B) an arrangement and a combination, respectively.
C) an arrangement and a permutation, respectively.
D) two combinations.
E) two arrangements.
Resolution
Alternative A
To differentiate arrangement and combination, it is necessary to analyze whether order matters in the grouping or not. Note that, in the first grouping, the order is irrelevant, as Group A is formed by the 4 teams drawn independently of the order, that is, there is, first, a combination.
Analyzing the second grouping, it is possible to see that the order matters in it, as the first team to be drawn will have the field command, which makes this grouping an arrangement.
In this way, the order is a combination and an arrangement.
Question 2 - A family composed of 7 adults, after deciding the itinerary of their trip, consulted an airline's website and found that the flight for the chosen date was almost full. In the figure, available on the website, the occupied seats are marked with an X and the only available seats are in white.
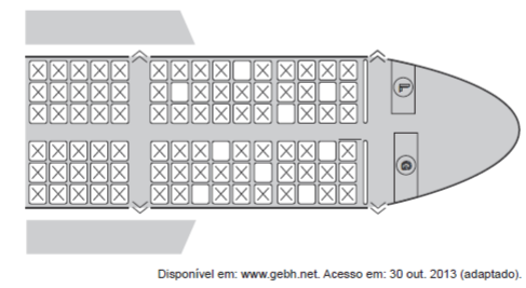
The number of different ways to accommodate the family on this flight is calculated by:
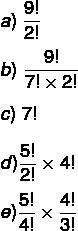
Resolution
Alternative B. In analyzing the situation, note that the order, ie which family member will sit in which chair, is not relevant. What matters are the 7 armchairs chosen by the family. So we are working with a combination. There are 9 seats free, and 7 will be chosen. so let's calculate the combination from 9 to 7. Substituting in the formula, we have to:
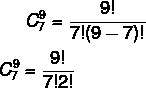
By Raul Rodrigues de Oliveira
Maths teacher
Source: Brazil School - https://brasilescola.uol.com.br/matematica/combinacao-simples.htm

