THE number line it is essentially a line where all the real numbers are marked and ordered. This is done so that no real number is used twice on the line or that no point on the line represents two positive real numbers.
Building a number line:
To build a number line, three steps must be followed:
1 – Take any straight line and mark a point on it that will have the value 0 (zero) and will be called origin.
2 – Starting from the origin, choose one increasing positive direction on the number line. For example, assuming the direction chosen is left to right (as is done in all Math books), the numbers to the right of zero will be positive and the numbers to the left will be negative. Furthermore, any number x to the left of a number y will obey the relationship x < y.
3 – Choose a measurement unit and mark all the whole numbers on the line (the possible ones, because the lines are infinite). Thus, if the unit of measurement is the centimeter, mark the values: - 1 cm, - 2 cm, 0, 1 cm, 2 cm, etc.
Once this is done, the number line will be ready for use. Any real number can be found on it and, if constructed as per the examples above, it can be compared to a ruler.
Formalization of a number line:
Given any line, each interval between two points belonging to this line is called a line segment.
Each line segment is assigned a positive real number, called the segment length.. This is what allows us to establish a relationship between the real numbers and the line. This relationship is called bi-univocal, as it is a function that takes each point on the line to a single real number. Considering the line segment that starts at the origin and ends at point A, of the x coordinate, its length will always be expressed by a real number obtained by |x – 0| or just |x|. The example below is a segment AB of length 10 taken on a number line:

Segment measurement starting at 0 and ending at point 10
This function is, in a way, bijector. Each point on the line is represented by a unique real number and, furthermore, there is no real number that is not represented by a point on the line or any point on the line that is not represented by a number real. This relationship between straight and real numbers is what defines thenumber line.
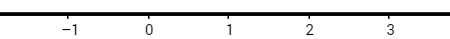
Example of a number line containing the origin and explaining the positive orientation
Equipment that can represent this relationship bi-univocal and the ruler. This object is used to draw straight lines and is graduate so that each distance is assigned a real number. However, its accuracy is limited, causing those who use it to assign measurements to limit themselves to using rational numbers, which are also real numbers.
By Luiz Paulo Moreira
Graduated in Mathematics
Source: Brazil School - https://brasilescola.uol.com.br/o-que-e/matematica/o-que-e-reta-numerica.htm

