Rationalization of denominators is the technique used when a fraction has an irrational number in the denominator and you want to find a second fraction equivalent to the first fraction, but which does not have an irrational number in its denominator. To do this, it is necessary to perform mathematical operations to rewrite the fraction so that it does not have an inexact root in its denominator.
Read too: How to solve operations with fractions?
How to rationalize denominators?

We'll start with the simplest case of rationalizing denominators and move on to the most complex, but the technique itself is to look for a equivalent fraction multiplying the numerator and denominator by a convenient number that allows eliminating the root of the denominator of the fraction. See how to do this in different situations below.
Rationalization when there is a square root in the denominator
There are some fractions that can be represented with irrational numbers in the denominators. See some examples:

When the fraction denominator is irrational, we use some techniques to transform it into a rational denominator, such as rationalization. when there is a
square root in the denominator, we can divide into two cases. The first one is when the fraction has only one root in its radical.Example 1:

To rationalize this denominator, let's find the fraction equivalent to this one, but which doesn't have an irrational denominator. For this, let's multiply numerator and denominator by the same number — in this case, it will be exactly the denominator of the fraction, that is, √3.

At multiplication of fractions, we multiply straight. We know that 1 · √3 = √3. In the denominator, we have that √3 ·√3 = √9 = 3. With that, we come to the following:

Hence, we have a representation of the fraction whose denominator is not an irrational number.
Example 2:
The second case is when there is a addition or a difference between an inexact root.

When there is a difference or an addition of terms in the denominator, one of them being the non-exact root, we multiply the numerator and the denominator by the conjugate of the denominator. We call the conjugate of √2 – 1 the inverse of the second number, that is, √2 + 1.
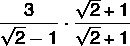
Performing the multiplication in the numerator, we have to:
3(√2 + 1) = 3√2 +3
The denominator is the remarkable product known as product of sum for difference. Its result is always the square of the first term minus the square of the second term.
(√2 – 1)(√2 + 1) = √2² – 1²
(√2 – 1)(√2 + 1) = √4 – 1²
(√2 – 1)(√2 + 1) = 2 – 1
(√2 – 1)(√2 + 1) = 1
So, rationalizing the denominator of this fraction, we have to:

See too: Three Common Mistakes in Algebraic Fraction Simplification
Rationalization when there is an index root greater than 2
Now look at some examples when there is in the denominator a root of indices greater than 2.
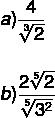
Since the goal is to eliminate the radical, let's multiply the denominator so that the root of that denominator can be canceled out.
Example 1:

In this case, to eliminate the exponent of the radical, let's multiply by the cubic root of 2² in the numerator and denominator, so that it appears inside the radical 2³ and, thus, it is possible to cancel the cubic root.
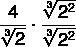
By carrying out the multiplication, we have to:

Example 2:

Using the same reasoning, let's multiply the denominator and numerator by a number that causes the potency from the denominator to the index, that is, let's multiply by fifth root of 3 cubed so that you can cancel the denominator.

Read too: How to simplify algebraic fractions?
solved exercises
question 1 – Rationalizing the denominator of the fraction below, we find:

A) 1 + √3.
B) 2(1 + √3).
C) – 2(1+ √3).
D) √3.
E) √3 –1.
Resolution
Alternative C.

Question 2 - (IFCE 2017 — adapted) Approximating the values of √5 and √3 to the second decimal place, we obtain 2.23 and 1.73, respectively. Approximately, the value of the following numeric expression to the second decimal place is:

A) 1.98.
B) 0.96.
C) 3.96.
D) 0.48.
E) 0.25.
Resolution
Alternative E.

By Raul Rodrigues de Oliveira
Maths teacher
Source: Brazil School - https://brasilescola.uol.com.br/matematica/racionalizacao-denominadores.htm
