The natural numbers arose from man's need to relate objects to quantities, the elements that belong to this set are:
N = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, ...}, zero came later, in order to express something null in positional filling.
The set of natural numbers appeared simply for the purpose of counting, in commerce its use came up against situations in which it was necessary to express losses. The mathematicians of the time, in order to solve this situation, created the set of whole numbers, symbolized by the letter Z.
Z = {..., -4,-3,-2,-1,0,1,2,3,4,... }
Commercial operations representing profit or loss could be calculated, for example:
20 – 25 = – 5 (loss)
–10 + 30 = 20 (profit)
–100 + 70 = – 30 (loss)
With the evolution of calculations, the set of whole numbers was not satisfying some operations, so a new numerical set was stipulated: the set of rational numbers. This set consists of the union between the set of natural numbers with whole numbers plus numerals that can be written in the form of fractions or decimal numbers.
Q = {..., -5;...; - 4,7;...; - 2;...; -1;...; 0;...; 2,65;...; 4;... }
Some decimal numbers cannot be written as a fraction, so they don't belong to the set of rationals, they form the set of irrational numbers. This set has important numbers for Mathematics, such as the number pi (~3.14) and the golden number (~1.6).
The union of the sets of Natural, Integer, Rational and Irrational numbers form the set of Real numbers.
The creation of the set of Real numbers took place throughout the entire Mathematics evolution process, meeting the needs of society. In the search for new discoveries, mathematicians ran into a situation arising from the resolution of a 2nd degree equation. Let's solve the equation x² + 2x + 5 = 0 by applying Bhaskara's Theorem:

Note that when developing the theorem we are faced with the square root of a negative number, making it impossible to solve within the set of Real numbers, as there is no negative number squared to result in number negative. The resolution of these roots was only possible with the creation and adaptation of complex numbers, by Leonhard Euler. Complex numbers are represented by the letter C and better known as the number of the letter i, being designated in this set the following reasoning: i² = -1.
These studies led mathematicians to calculate the roots of negative numbers, because using the term i² = -1, also known as imaginary number, it is possible to extract the square root of numbers negative. Observe the process: 
Complex numbers are the largest number set in existence.
N: set of Natural numbers
Z: set of integer numbers
Q: set of Rational numbers
I: set of irrational numbers
R: set of real numbers
C: set of Complex numbers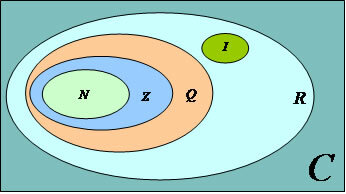
by Mark Noah
Graduated in Mathematics
Brazil School Team
Complex numbers - Math - Brazil School
Source: Brazil School - https://brasilescola.uol.com.br/matematica/conjunto-dos-numeros-complexos.htm
