►Single set and empty set
For example:
A = { x | x is even and 4 < x < 8 } or A = {6}
B = { x | 2x + 1 = 7 and x is integer } or B = {3}
The two sets above are examples of unitary sets. Because they have only one element.
Given the set C = { y | y is natural and 2 < y < 3 } is a set that has no elements, this type of set is called a empty set.
We indicate an empty set by { } or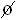 
, never by { 
}.
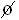►Iequality of sets
We say that one set is equal to another if all the elements in one set are equal to all the elements in the other set.
Example:
given the sets A = {0,1,2,3,4} and B = {2,3,4.1,0} as all elements are equal we can say that A = B.
►Relation between two sets.
When we are going to do the element-to-set relationship, we use the symbols of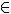 
belongs and 
does not belong.
For example:
Given the set of natural numbers the element 5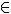 
N
and
-8 
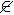N.
Now when we relate set to set we use the symbols of 
is contained and 
it is not contained.
For example:
{1,2,3}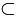 
{1,2,3,4,5,6}
The set of N is contained within the integers. N
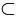Z and the set of integers is not contained within the set of naturals Z 
No. ♦ Every set is contained within itself B B.
♦ The empty set is contained in every set A.
by Danielle de Miranda
Graduated in Mathematics
Brazil School Team
Set - Math - Brazil School
Source: Brazil School - https://brasilescola.uol.com.br/matematica/notacoes-importantes-sobre-conjunto.htm