In going through the concepts of determinants, we learn forms and procedures that help to find the determinants of square matrices of order 3. Chió's rule allows us to calculate the determinant of a matrix of order n, using a matrix of lower order (order n-1).
However, to use this rule it is necessary that the element a11 be equal to 1. If this happens, we can use the steps in this rule. Look:
• Delete the first row and first column of the matrix.
• From the remaining elements, subtract the product of the two suppressed elements (one in the row and the other in the column) corresponding to this remaining element. For example, in element a23 you will take the product of the element in the second row of the column that was suppressed by the element of the third column of the row that was suppressed.
• With the results of the subtractions performed in the previous step, a new matrix will be obtained, a matrix with a lower order, however with a determinant equal to the original matrix.
See the example below.

From each element of the new matrix we will subtract the product of the suppressed elements (colored elements).
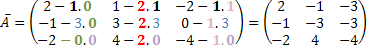
Do not stop now... There's more after the advertising ;)
Note that the calculation of the determinant of this new matrix can be done by Sarrus' rule. This determinant will be the same as the initial matrix of order 4.
But remember that this rule can only be used if the element a11 is equal to 1, otherwise the row and column elements cannot be suppressed.
By Gabriel Alessandro de Oliveira
Graduated in Mathematics
Brazil School Team
Matrix and determinant- Math - Brazil School
Would you like to reference this text in a school or academic work? Look:
OLIVEIRA, Gabriel Alessandro de. "Matrix Determinant: Chió's Rule"; Brazil School. Available in: https://brasilescola.uol.com.br/matematica/determinante-matriz-regra-chio.htm. Accessed on June 29, 2021.

