The sum of the terms of a finite geometric progression is given by the expression:
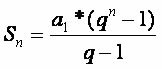, where q (ratio) is different from 1. Some cases in which the ratio q belongs to the interval –1 < q < 1, we verify that when the number of elements n approaches infinity (+∞), the expression whatno tends to zero value. Therefore, replacing whatno by zero in the expression of the sum of terms of a finite PG we will have an expression capable of determining the sum of terms of an infinite PG within the interval –1 < q < 1, note:
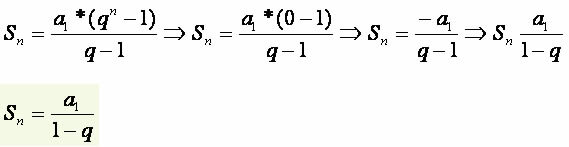
Example 1
Determine the sum of the elements of the following PG: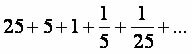 
.
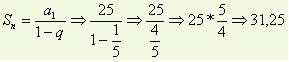
Example 2
The mathematical expression of the sum of terms of an infinite PG is recommended in obtaining the generating fraction of a simple or compound periodic decimal. Watch the demo.
Considering the simple periodic decimal 0.222222..., let's determine its generating fraction.
Example 3
Let's determine the fraction that gives rise to the following decimal number 0.231313..., classified as a composite periodic decimal.
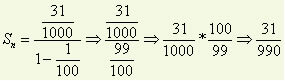
Example 4
Find the sum of the elements of the geometric progression given by (0.3; 0,03; 0,003; 0,0003; ...).
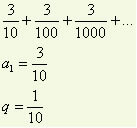
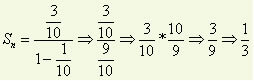
by Mark Noah
Graduated in Mathematics
Brazil School Team
Progressions - Math - Brazil School
Source: Brazil School - https://brasilescola.uol.com.br/matematica/soma-dos-termos-uma-pg-infinita.htm