Every square matrix can be associated with a number, which is obtained from calculations made between the elements of this matrix. This number is called determinant.
The order of the square matrix determines the best method for calculating its determinant. For matrices of order 2, for example, it is enough to find the difference between the product of the elements of the main diagonal and the product of the elements of the secondary diagonal. For 3x3 matrices, we can apply the Sarrus rule or even the Laplace's Theorem. It is worth remembering that the latter can also be used to calculate determinants of square matrices of order greater than 3. In specific cases, the calculation of the determinant can be simplified by just a few determinant properties.
To understand how the determinant is calculated with the Sarrus rule, consider the following matrix A of order 3:

Representation of an order 3 matrix
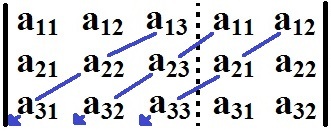
Initially, the first two columns are repeated to the right of matrix A:

We must repeat the first two columns to the right of the matrix
Then the elements of the main diagonal are multiplied. This process must also be done with the diagonals that are to the right of the main diagonal so that it is possible add the products of these three diagonals:
det AP = The11.The22.The33 + the12.The23.The31 + the13.The21.The32

We must add the products of the main diagonals
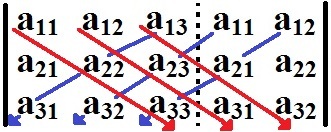
The same process must be carried out with the secondary diagonal and the other diagonals to its right. However, it is necessary subtract the products found:
Do not stop now... There's more after the advertising ;)
det As = - a13.The22.The31 - a11.The23.The33 - a12.The21.The33
We must subtract the products from the secondary diagonals
Joining the two processes, it is possible to find the determinant of matrix A:
det A = det AP + det As
det A = The11.The22.The33 + the12.The23.The31 + the13.The21.The32- a13.The22.The31 - a11.The23.The33 - a12.The21.The33
Representation of the application of the Sarrus Rule
Now see the calculation of the determinant of the following matrix B of order 3x3:

Calculation of the determinant of matrix B using the Sarrus Rule
Using Sarrus' rule, the calculation of the determinant of matrix B will be done as follows:

Applying Sarrus' Rule to Find the Determinant of Matrix B
det B = B11.B22.B33 + b12.B23.B31 + b13.B21.B32- B13.B22.B31 - B11.B23.B33 - B12.B21.B33
det B = 1.3.2 + 5.0.4 + (–2).8.(–1) – (–2).3.4 – 1.0.(–1) – 5.8.2
det B = 6 + 0 + 16 – (–24) – 0 – 80
det B = 22– 56
det B = – 34
Therefore, by Sarrus' Rule, the determinant of matrix B is – 34.
By Amanda Gonçalves
Graduated in Mathematics
Would you like to reference this text in a school or academic work? Look:
RIBEIRO, Amanda Gonçalves. "Rule of Sarrus"; Brazil School. Available in: https://brasilescola.uol.com.br/matematica/regra-sarrus.htm. Accessed on June 29, 2021.
Matrix, Determinant, System resolution, Cramer's rule, Cramer's rule application, How to apply Cramer's rule, Unknowns of a system.