Operations with complex numbers in trigonometric form facilitate calculation involving the elements of this set. Multiplication and division of complexes that are in trigonometric form are done almost instantly, while in algebraic form the process requires more calculations. The potentiation and radiciation of complexes in trigonometric form are also facilitated with the use of Moivre's formulas. Let's see how the rooting of these numbers is carried out:
Consider any complex number z = a + bi. The trigonometric form of z is: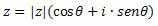
The n-index roots of z are given by the second Moivre formula:
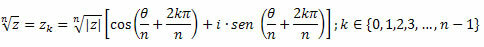
Example 1. Find the square roots of 2i.
Solution: First we must write the complex number in trigonometric form.
All of the complex number is of the form z = a + bi. So, we have to:
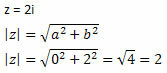
We also know that:
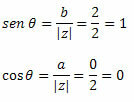
With the sine and cosine values we can conclude that:
Thus, the trigonometric form of z = 2i is: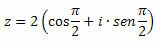
Now, let's calculate the square roots of z using Moivre's formula.
Since we want the square roots of z, we'll get two distinct roots z
For k = 0, we will have
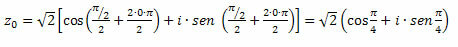
For k = 1, we will have:
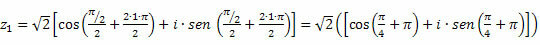
Or
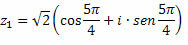
Example 2. Get the cubic roots of z = 1∙(cosπ + i∙senπ)
Solution: As the complex number is already in trigonometric form, just use Moivre's formula. From the statement we have that ø = π and |z| = 1. Thus,

We will have three distinct roots, z0, z1 and z2.
For k = 0
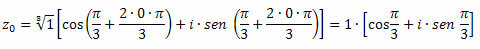
For k = 1
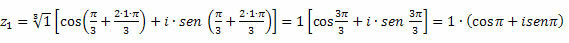
Or z1 = – 1, since cos π = – 1 and sin π = 0.
For k = 2

Do not stop now... There's more after the advertising ;)
By Marcelo Rigonatto
Specialist in Statistics and Mathematical Modeling
Brazil School Team
Complex numbers - Math - Brazil School
Would you like to reference this text in a school or academic work? Look:
RIGONATTO, Marcelo. "Radiciation of complex numbers in trigonometric form"; Brazil School. Available in: https://brasilescola.uol.com.br/matematica/radiciacao-numeros-complexos-na-forma-trigonometrica.htm. Accessed on June 29, 2021.