A area of the square is equal to the product of its base and its height. The square is a quadrilateral which has all equal sides, therefore, as its base and height have the same measurement, the area of the square is equal to the measurement of the side squared. In addition to the area, it is possible to calculate the length of the diagonal of the square and the measurement of its perimeter.
Read too: How to calculate the area of different plane figures
Summary about the area of the square
A square is a flat figure that has 4 sides of the same size.
To calculate the area of the square, we calculate the side measurement squared.
The formula for the area of a square is:
\(A=l^2\)
In addition to the area, we also have a formula to calculate the length of the diagonal of the square:
\(d=\sqrt2\)
The perimeter of the square can be calculated by the formula:
\(P=4l\)
What is the formula for the area of a square?
The square is a flat figure formed by 4 congruent sides, that is, the 4 sides of the square have the same measurement.

Knowing the side measurement of the square, to calculate the area simply calculate the square of the side measurement, that is:
\(\mathbf{A=l^2}\)
A → area measurement.
l → side length.
How is the area of a square calculated?
To calculate the area of a square, simply Substitute the length value of your side in place of the l in the formula.
Example 1:
A square has a side measuring 12 cm, so the area of this square is equal to:
Resolution:
Calculating the area, we have:
\(A=12^2\)
\(A=144\)
So, the area of this square is 144 cm².
Example 2:
Calculate the area of the square in the following image:

Resolution:
As the side measurement is 5 cm, to calculate the area we will square 5:
\(A=5^2\)
\(A= 25 \)
The area of this square is 25 cm².
See too: Triangle area — how to calculate it?
How to calculate the diagonal of a square?
The diagonal of the square is the straight line segment that connects two non-consecutive vertices of the square. The square has two diagonals, which are always the same length.
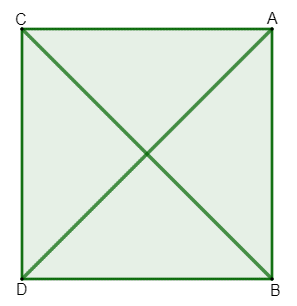
To calculate the diagonal measurement of the square, we can apply the Pythagorean theorem:

\(d^2=l^2+l^2\)
\(d^2=2l^2\)
\(d=\sqrt{2l^2 }\)
Note that, as a consequence of Pythagoras' theorem, the length of the diagonal of the square with a side measuring lcan be calculatedby the formula:
\(d=l\sqrt2\)
Example:
What is the length of the diagonal of a square that has sides measuring 3 cm?
Resolution:
If l = 3, then we have:
\(d=3\sqrt2\)
Therefore, the length of the diagonal of this square is \(d=3\sqrt2\) cm.
What is the difference between the area of a square and the perimeter of a square?
The difference between the area and the perimeter, whether of the square or of any other polygon, is that area is a measurement that has two dimensions, which is the space that that area occupies in the plane. Already the perimeter is a measurement that has a single dimension, which is the contour of the polygon. To calculate the perimeter, we add up all the sides of the polygon.
In the square of sides measuring l, To calculate the perimeter we have to:
\(\mathbf{P = 4l}\)
Example:
A square has sides measuring 3 cm, so what is the measurement of its area and perimeter?
Resolution:
First, we will calculate the area of this square. We know that:
\(A=l^2\)
\(A=3^2\)
\(A= 9 \)
The area is 9 cm².
Now, we will calculate the perimeter of this square:
\(P=4l\)
\(P=4⋅3\)
\(P = 12 \)
The perimeter of this polygon is 12 cm.
Know more: How do you know how many diagonals a polygon has?
Solved exercises on the area of a square
Question 1
A region is shaped like a square with a side measuring 18 m. So, we can say that the area of this region is:
A) 72 m²
B) 108 m²
C) 144 m²
D) 288 m²
E) 324 m²
Resolution:
Alternative E
Calculating the area, we have:
\(A=l^2\)
\(A=18^2\)
\(A=324\ m^2\)
Question 2
Mr. Antônio decided to give his two sons a piece of land each. As he is a very fair person, he consulted both, so that the area of these lands was the same. If your first child's land is rectangular, with sides measuring 48 meters and 12 meters, and knowing If your second child's land is a square, then the measurement of the sides of the second child's land é:
A) 20 meters
B) 22 meters
C) 24 meters
D) 30 meters
E) 32 meters
Resolution:
Alternative C
Calculating the area of the rectangular plot, we have:
\(A = 48 ⋅12 = 576\)
As the second child's land has the same area, but is in the shape of a square, we have:
\(l^2=576\)
\(l=\sqrt{576}\)
\(l=24 \)
Source
DANTE, Luiz Roberto. Mathematics: Context & Applications. 8th year. São Paulo: Editora Ática, 2021.