Practice on the equations of the line with the solved and commented exercises, clear your doubts and be ready for evaluations and entrance exams.
Line equations belong to the area of mathematics called analytic geometry. This field of study describes points, lines and shapes in the plane and in space, through equations and relationships.
The slope of the line passing through points A (0.2) and B (2.0) is
a) -2
b) -1
c) 0
d) 2
e) 3
Calculate the value of t, knowing that the points A (0, 1), B (3, t) and C (2, 1) are collinear.
to 1
b) 2
c) 3
d) 4
e) 5
The three-point alignment condition says that the determinant of the matrix equals zero.
By Sarrus rule:
0.t.1 + 1.1.2 + 1.3.1 - (2.t.1 + 1.1.0 + 1.3.1) = 0
0 + 2 + 3 - (2t + 0 + 3) = 0
5 - 2t - 3 = 0
2 = 2t
t = 1
The coefficients, angular and linear, of the line x - y + 2 = 0 are, respectively,
a) Angular coefficient = 2 and linear coefficient = 2
b) Angular coefficient = -1 and linear coefficient = 2
c) Angular coefficient = -1 and linear coefficient = -2
d) Angular coefficient = 1 and linear coefficient = 2
e) Angular coefficient = 2 and linear coefficient = 2
Writing the equation in reduced form, we have:
The slope is the number that multiplies x, so it's 1.
The linear coefficient is the independent term, so it is 2.
Obtain the equation of the line that has the graph below.
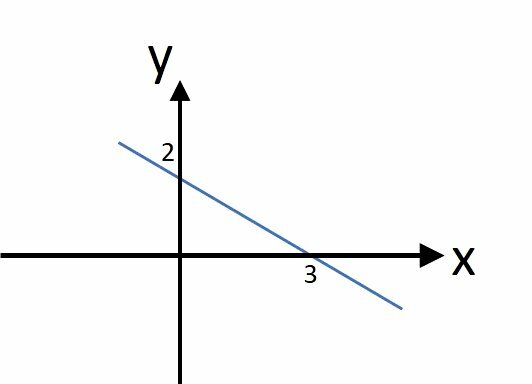
a) x + y - 6 = 0
b) 3x + 2y - 3 = 0
c) 2x + 3y - 2 = 0
d) x + y - 3 = 0
e) 2x + 3y - 6 = 0
The points where the line cuts the axes are (0, 2) and (3, 0).
Using the parametric form:
As the answer options are in general form, we must perform the sum.
Calculate the least common multiple to equal the denominators.
MMC(3, 2) = 6
Find the coordinates of the point of intersection between the line r: x + y - 3 = 0 and the line passing through the points A(2, 3) and B(1, 2).
a) (3, 2)
b) (2, 2)
c) (1, 3)
d) (2, 1)
e) (3, 1)
Determine the line passing through points A and B.
Calculation of the angular coefficient:
So the line is:
The intersection point is the solution of the system:
Adding the equations:
Substituting in the first equation:
So the coordinates of the point where the lines intersect is (2, 1)
(PUC - RS) The straight line r of equation y = ax + b passes through the point (0, –1), and, for each unit of variation of x, there is a variation in y, in the same direction, of 7 units. Your equation is
a) y = 7x – 1.
b) y = 7x + 1.
c) y = x – 7.
d) y = x + 7.
e) y = –7x – 1.
A change of 1 in x causes a change of 7 in y. This is the definition of slope. Therefore, the equation must have the form:
y = 7x + b
Since the point (0, -1) belongs to the line, we can substitute it into the equation.
In this way, the equation is:
(IF-RS 2017) The equation of the line that passes through the points A(0,2) and B(2, -2) is
a) y = 2x + 2
b) y = -2x -2
c) y = x
d) y = -x +2
e) y = -2x + 2
Using the reduced equation and the coordinates of point A:
Using the coordinates of point B and substituting the value of b = 2:
Setting up the equation:
(UNEMAT 2017) Let r be a straight line with equation r: 3x + 2y = 20. A line s intersects it at the point (2,7). Knowing that r and s are perpendicular to each other, what is the equation of the line s?
a) 2x − 3y = −17
b) 2x − 3y = −10
c) 3x + 2y = 17
d) 2x − 3y = 10
e) 2x + 3y = 10
Since the lines are perpendicular, their slopes are:
To determine the slope of r, we change the equation from general to reduced form.
The slope is the number that multiplies the x, being -3/2.
Finding the coefficient of the line s:
As the lines intersect at the point (2, 7), we substitute these values in the equation of the line s.
Setting up the reduced equation of the line s:
Since the answer choices are in general form, we need to convert.
(Enem 2011) A visual programmer wants to modify an image, increasing its length and maintaining its width. Figures 1 and 2 represent, respectively, the original image and the one transformed by doubling the length.
To model all the transformation possibilities in the length of this image, the programmer needs to discover the patterns of all the lines that contain the segments that outline the eyes, nose and mouth and then elaborate the program.
In the previous example, the segment A1B1 of figure 1, contained in line r1, became the segment A2B2 of figure 2, contained in line r2.
Suppose that, keeping the width of the image constant, its length is multiplied by n, where n is an integer and positive number, and that, in this way, the line r1 undergoes the same transformations. Under these conditions, the segment AnBn will be contained in the line rn .
The algebraic equation that describes rn, in the Cartesian plane, is
a) x + ny = 3n.
b) x - ny = - n.
c) x - ny = 3n.
d) nx + ny = 3n.
e) nx + 2ny = 6n.
Finding the line r1 in the original figure:
Its angular coefficient is:
The line cuts the y-axis at the point (0, 3), so its equation is:
Finding the line r2 in the modified figure:
Its angular coefficient is:
The line also cuts the y-axis at the point (0, 3), so its equation is:
From the original figure equation to the modified one, the coefficient of y and the independent term were multiplied by 2.
So, for other proportions:
