O truncated cone volume is the space occupied by this round body. Since the cross section of a cone of radius R produces a smaller cone of radius r and a truncated cone, the volumes of these three solids are related.
Read too: How to Calculate the Trunk of a Pyramid
Summary on the volume of the truncated cone
- A cone of radius R cut transversely at height H of the base plane is divided into two geometric solids: a cone of radius r It is a trunk cone.
- The main elements of the truncated cone are the height H, the smallest base of radius r and larger base of radius R.
- The volume of the truncated cone is the difference between the volume of the cone of radius R and the volume of the cone of radius r.
- The formula for the volume of the truncated cone is:
\(V_t=\frac{1}{3} πh (R^2+r^2+Rr)\)
Video lesson on the volume of the truncated cone
What are the elements of the truncated cone?
The elements of a truncated cone formed from the section of a right cone of radius R are:
- minor base – radius circle r, obtained in the section of the cone of radius R .
- larger base – circular base of the cone of radius R .
- Height (h) – distance between the planes of the bases.
- Generatrix – segment with ends on the circumferences that delimit the bases.
A image below presents the elements of a truncated cone. Note that the minor and major bases are parallel.

Trunk of Cone Volume Formula
Next, let's deduce the formula for the volume of a frustum of height H, smaller base radius r and radius of the largest base R .
Consider that the cross section of a cone of radius R and height H1 produces two solids:
- a lightning cone r and height h2 It is
- a tall trunk cone H .
realize that \(H_1=H_2+h\).
The volume of the cone of radius R (which we will call the larger cone) will be represented by VR; the volume of the radius cone r (which we will call the smaller cone), by Vr; and the volume of the truncated cone by Vt. Therefore:
\(V_R=V_r+V_t\)
Note that:
- \( V_R=\frac{1}{3} πR^2 H_1=\frac{1}{3} πR^2 (H_2+h)\)
- \( V_r=\frac{1}{3}1/3 πr^2 H_2\)
Observation: VR and Vr are volumes of cones. To review this matter, click here.
Like this:
\(V_R=V_r+V_t\)
\(\frac{1}{3} πR^2 (H_2+h)=1/3 πr^2 H_2+V_t\)
\(V_t=\frac{1}{3} πR^2 (H_2+h)-1/3 πr^2 H_2\)
\(V_t=\frac{1}{3} πR^2 H¬_2+1/3 πR^2 h-1/3 πr^2 H_2\)
\(V_t=\frac{1}{3} π(R^2 H_2+R^2 h-r^2 H_2 )\)
\(V_t=\frac{1}{3} π[R^2 h+(R^2-r^2 ) H_2 ]\)
The H2 term corresponds to the height of the smaller cone. Relating the heights of the cones with the respective radii of the bases, we can obtain a formula for the volume of the trunk that depends only on the elements of the trunk (R, r It is H).
Associating the radius and height of the larger cone (R and H1 ) with the radius and height of the smaller cone (r and H2), we have the following proportion:
\(\frac{R}{H_1}=\frac{r}{H_2}\)
\(\frac{R}{H_2+h}=\frac{r}{H_2}\)
\(RH_2=rH_2+rh\)
\(H_2=\frac{rh}{R-r}\)
Soon, we can rewrite the trunk volume Vt as follows:
\(V_t=\frac{1}{3} π[R^2 h+(R^2-r^2 ) H_2 ]\)
\(V_t=\frac{1}{3} πh[R^2h+(R^2-r^2 ) \frac{rh}{R-r}]\)
\(V_t=\frac{1}{3} πh[R^2+(R^2-r^2 ) \frac{r}{R-r}]\)
\(V_t=\frac{1}{3} πh[R^2+(R+r)(R-r) \frac{r}{R-r}]\)
\(V_t=\frac{1}{3} πh[R^2+(R+r) r]\)
Like this, The formula for the volume of the truncated cone is:
\(V_t=\frac{1}{3}πh (R^2+r^2+Rr)\)
Read too: Volume formulas of various geometric solids
How to calculate the volume of the truncated cone?
To calculate the volume of a truncated cone, just substitute the measurements of the height, the radius of the smaller base and the radius of the larger base in the formula.
- Example: What is the volume, in cubic centimeters, of a truncated cone in which the radius of the larger base is R = 5 cm, the radius of the smaller base is r = 3 and the height is h = 2 cm? (Use π=3 )
Substituting the data in the formula, we have:
\(V_t=\frac{1}{3}⋅3⋅2⋅(5^2+3^2+5⋅3)\)
\(V_t=2⋅(49)\)
\(V_t=98 cm³\)
Solved exercises on the volume of the truncated cone
question 1
A pot has the shape of a truncated cone with the largest base radius R = 8 cm, the smallest base radius r = 4 and the height h = 2 cm. The volume of this pot, in cm³, is:
a) 48 pi
b) 64 pi
c) 112 pi
d) 448 pi
e) 1344 pi
Resolution
Substituting the data in the formula, we have:
\(V_t=\frac{1}{3}⋅π⋅12⋅(8^2+4^2+8⋅4)\)
\(V_t=4π⋅(112)\)
\(V_t=448 π\)
Alternative D
question 2
(Enem 2021) One person bought a mug to drink soup, as illustrated.
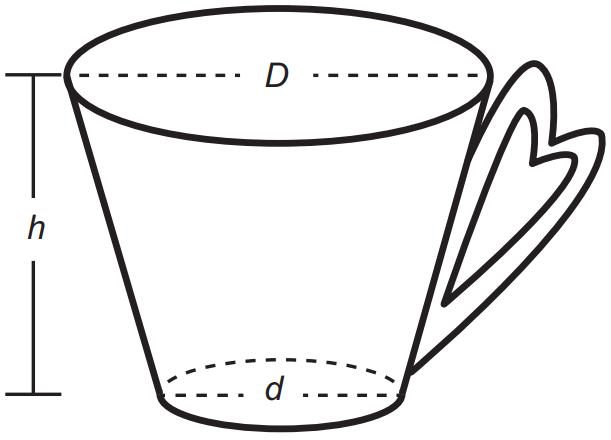
It is known that 1 cm³ = 1 mL and that the top of the mug is a circle with a diameter (D) measuring 10 cm, and the base is a circle with a diameter (d) measuring 8 cm.
Furthermore, it is known that the height (h) of this mug measures 12 cm (distance between the center of the top and bottom circles).
Use 3 as an approximation for π.
What is the volumetric capacity, in milliliters, of this mug?
a) 216
b) 408
c) 732
d) 2196
e) 2928
Resolution
The shape of the mug is a truncated cone in which the top is the larger base. Also, R=5, r = 4 cm and H = 12. Soon:
\(V_t=\frac{1}{3} πh (R^2+r^2+Rr)\)
\(V_t=\frac{1}{3}⋅3⋅12⋅(5^2+4^2+5⋅4)\)
\(V_t=12⋅(61)\)
\(V_t=732 cm³\)
As 1 cm³ = 1 mL, we have 732 cm³ = 732 mL.
Alternative C
Sources:
DANTE, L. R. Mathematics: context & applications - High school. 3. ed. Sao Paulo: Attica, 2016. v.3.
DOLCE, O; POMPEO, J. No. Fundamentals of Elementary Mathematics, Vol 10: Spatial Geometry - Position and Metric. 7 ed. Santos: Current, 2013.
Source: Brazil School - https://brasilescola.uol.com.br/matematica/volume-do-tronco-de-cone.htm