A identity matrix is a special kind of headquarters. We know as identity matrix In the square matrix of order n that has all terms on the diagonal equal to 1 and terms not belonging to the main diagonal equal to 0. The identity matrix is considered the neutral element of multiplication, that is, if we multiply a matrix M by the identity matrix, we find as a result the matrix itself M.
See too: What is the determinant of a matrix?
Summary about identity matrix
The identity matrix is the square matrix with main diagonal elements equal to 1 and with the other elements equal to 0.
There are identity matrices of different orders. We represent the identity matrix of order n by I n.
The identity matrix is the neutral element of matrix multiplication, that is, \( A\cdot I_n=A.\)
The product of a square matrix and its inverse matrix is the identity matrix.
What is identity matrix?
The identity matrix is a special type of square matrix. A square matrix is known as an identity matrix if it has all elements on the main diagonal equal to 1 and all other elements equal to 0. Then, in every identity matrix:
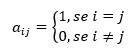
➝ Identity matrix types
There are identity matrices of different orders. the order n is represented by In. Let's see below some matrices of other orders.
Order 1 identity matrix:
\(I_1=\left[1\right]\)
Order 2 identity matrix:
\(I_2=\left[\begin{matrix}1&0\\0&1\\\end{matrix}\right]\)
Order 3 identity matrix:
\(I_3=\left[\begin{matrix}1&0&0\\0&1&0\\0&0&1\\\end{matrix}\right]\)
Order 4 identity matrix:
\(I_4=\left[\begin{matrix}1&0&0&0\\0&1&0&0\\0&0&1&0\\0&0&0&1\\\end{matrix}\right]\)
Order 5 identity matrix:
\(I_5=\left[\begin{matrix}1&0&0&0&0\\0&1&0&0&0\\0&0&1&0&0\\0&0&0&1&0\\0&0&0&0&1\\\end{matrix}\right]\)
Successively, we can write identity matrices of different orders.
Identity matrix properties
The identity matrix has an important property, as it is the neutral element of the multiplication between the matrices. This means that any matrix multiplied by the identity matrix is equal to itself. Thus, given the matrix M of order n,we have:
\(I_n\cdot M=M\cdot I_n=M\)
Another important property of the identity matrix is that the product of a square matrix and its inverse matrix is the identity matrix. Given a square matrix M of order n, the product of M by its inverse is given by:
\(M\cdot M^{-1}=I_n\)
Read too: What is a triangular matrix?
Multiplication of the identity matrix
When we multiply a matrix M by the identity matrix of order n, we get the matrix M as a result. Let's see, below, an example of the product of the matrix M of order 2 by the identity matrix of order 2.
\(A\ =\ \left(\begin{matrix}a_{11}&a_{12}\\a_{21}&a_{22}\\\end{matrix}\right) \) It is \(I_n=\left(\begin{matrix}1&0\\0&1\\\end{matrix}\right)\)
Suposing that:
\(A\cdot I_n=B\)
We have:
\(B\ =\left(\begin{matrix}b_{11}&b_{12}\\b_{21}&b_{22}\\\end{matrix}\right)\)
So the product of A by \(I_n\) it will be:
\(b_{11}=1\cdot a_{11}\cdot1+0\cdot a_{12}=a_{11}\)
\(b_{12}=0\cdot a_{11}+1\cdot a_{12}=a_{12}\)
\(b_{21}=1\cdot a_{21}+0\cdot a_{22}=a_{21}\)
\(b_{22}=0\cdot a_{21}+1\cdot a_{22}=a_{22}\)
Note that the terms of matrix B are identical to the terms of matrix A, that is:
\(A\cdot I_n=\left[\begin{matrix}a_{11}&a_{12}\\a_{21}&a_{22}\\\end{matrix}\right]=A\)
Example:
Being M The matrix \(M=\ \left[\begin{matrix}1&4&0\\2&5&3\\-3\ &-2&1\\\end{matrix}\right]\), calculate the product between the matrix M and the matrix \(I_3\).
Resolution:
Carrying out the multiplication, we have:
\(M\cdot I_3=\left[\begin{matrix}1&4&0\\2&5&3\\-3\ &-2&1\\\end{matrix}\right]\cdot\left[\begin{matrix}1&0&0\\ 0&1&0\\0&0&1\\\end{matrix}\right]\)
\(M\cdot I_3=\left[\begin{matrix}1\ \cdot\ 1\ +\ 0\ \cdot\ 4\ +\ 0\ \cdot\ 0&1\cdot0\ +\ 4\ \cdot\ 1 \ +\ 0\cdot\ 0&1\cdot0+4\cdot0+0\cdot1\\2\cdot\ 1\ +\ 5\ \cdot\ 0\ +\ 3\ \cdot\ 0&2\ \cdot\ 0\ +\ 5\cdot1+3\cdot0&2\cdot0+5\cdot0+3\cdot1\\-3\cdot1+\left(-2\right)\cdot0+1\cdot0&-3\cdot0+\left(-2\right)\ cdot1+1\cdot0&-3\cdot0+\left(-2\right)\cdot0+1\cdot1\\\end{matrix}\right]\)
\(M\cdot I_3=\left[\begin{matrix}1&4&0\\2&5&3\\-3\ &-2&1\\\end{matrix}\right]\)
Solved exercises on identity matrix
question 1
There is a square matrix of order 3 which is defined by \(a_{ij}=1 \) when \(i=j\) It is \(a_{ij}=0\) It is when \(i\neq j\). This matrix is like:
A) \( \left[\begin{matrix}1&1&1\\1&1&1\\1&1&1\\\end{matrix}\right]\)
B) \( \left[\begin{matrix}0&0&1\\0&1&0\\1&0&0\\\end{matrix}\right]\)
W) \( \left[\begin{matrix}0&1&1\\0&0&1\\0&0&1\\\end{matrix}\right]\)
D) \( \left[\begin{matrix}1&0&0\\0&1&0\\0&0&1\\\end{matrix}\right]\)
AND) \( \left[\begin{matrix}1&0&0\\1&1&0\\1&1&1\\\end{matrix}\right]\)
Resolution:
Alternative D
Analyzing the matrix, we have:
\(a_{12}=a_{13}=a_{21}=a_{23}=a_{31}=a_{32}=0\)
\(a_{11}=a_{22}=a_{33}=1\)
So, the matrix is equal to:
\(\left[\begin{matrix}1&0&0\\0&1&0\\0&0&1\\\end{matrix}\right]\)
question 2
(UEMG) If the inverse matrix of \(A=\left[\begin{matrix}2&3\\3&x\\\end{matrix}\right]\) é \( \left[\begin{matrix}5&-3\\-3&2\\\end{matrix}\right]\), the value of x is:
A) 5
B) 6
C) 7
D) 9
Resolution:
Alternative A
Multiplying the matrices, we realize that their product is equal to the identity matrix. Calculating the product of the second row of the matrix by the first column of its inverse, we have:
\(3\cdot5+x\cdot\left(-3\right)=0\)
\(15-3x=0\)
\(-\ 3x=0-15\ \)
\(-\ 3x=-\ 15\)
\(x=\frac{-15}{-3}\)
\(x=5\ \)
By Raul Rodrigues de Oliveira
Maths teacher
Source: Brazil School - https://brasilescola.uol.com.br/matematica/matriz-identidade.htm