A elastic potential energy it's a kind of potential energy linked to the elastic properties of materials, whose compression or elasticity is capable of producing the movement of bodies. Its unit of measurement is the Joule, and it can be calculated by the product between the elastic constant and the square of the deformation suffered by the elastic object, divided by two.
Know more: Electric potential energy — a form of potential energy that requires the interaction of electric charges
Elastic potential energy summary
A energy Elastic potential is a form of potential energy associated with the deformation and elongation of elastic bodies.
Its calculation formula is as follows:
\(E_{pel}=\frac{k\cdot x^2}2\)
It can also be calculated by the formula that relates the elastic potential energy to the elastic force:
\(E_{pel}=\frac{F_{pel}\cdot x}2\)
At physical, energy is always conserved, never generated or destroyed.
It is possible to transform elastic potential energy into gravitational potential energy and/or kinetic energy.
Elastic potential energy converts to kinetic energy more slowly than gravitational potential energy would.
Gravitational potential energy is related to the height variation of bodies located in a region with gravitational field.
What is elastic potential energy?
The elastic potential energy is one physical quantity scaling related to the action produced by elastic materials or flexible on other bodies. Examples of elastic or flexible materials are springs, rubbers, elastics. It is one of the forms of potential energy, just like gravitational potential energy.
According to the International System of Units (SI), Its unit of measurement is the Joule., represented by the letter J.
She is directly proportional to the elastic constant and the deformation suffered by elastic objects, therefore, as they increase, the elastic potential energy also increases.
Elastic potential energy formulas
→ Elastic potential energy
\(E_{pel}=\frac{k\cdot x^2}2\)
\(E_{pel}\) → elastic potential energy, measured in Joules \([J]\).
k → elastic constant, measured in Newton per meter \([N/m]\).
x → deformation of the object, measured in meters\([m]\).
Example:
Determine the elastic potential energy in a spring that is strained by 0.5 m knowing that its spring constant is 200 N/m.
Resolution:
We will calculate the elastic potential energy using its formula:
\(E_{pel}=\frac{k\cdot x^2}2\)
\(E_{pel}=\frac{200\cdot 0.5^2}2\)
\(E_{pel}=\frac{200\cdot 0.25}2\)
\(E_{pel}=25\ J\)
The elastic potential energy is 25 Joules.
→ Elastic potential energy related to elastic force
\(E_{pel}=\frac{F_{pel}\cdot x}2\)
\(E_{pel}\) → elastic potential energy, measured in Joules \([J]\).
\(Gall}\) → elastic force, that is, the force exerted by the spring, measured in Newton \([N]\).
x → deformation of the object, measured in meters \([m]\).
Example:
What is the elastic potential energy in a spring that is strained by 2.0 cm when subjected to a force of 100 N?
Resolution:
First we will convert the deformation from centimeters to meters:
20 cm = 0.2 m
Then we will calculate the elastic potential energy by the formula that relates it to elastic force:
\(E_{pel}=\frac{F_{pel}\cdot x}2\)
\(E_{pel}=\frac{100\cdot0,2}2\)
\(E_{pel}=10\ J\)
The elastic potential energy is 10 Joules.
Applications of elastic potential energy
The applications of elastic potential energy mainly refer to its transformation into other forms of energy or to the storage of kinetic energy. Below we will see some everyday examples of its applications.
Car bumpers are designed to deform when they suffer an impact, storing the maximum amount of kinetic energy and converting it into elastic potential energy.
In the trampoline, we have the deformation of the springs and the elastic material, causing an energy elastic potential that will later be converted into kinetic energy and potential energy gravitational.
Some sneakers have springs that reduce the impact suffered by the movement, in which kinetic energy is being transformed into elastic potential energy.
Transformation of elastic potential energy
Elastic potential energy obeys the principle of conservation of energy, in which energy is always conserved and cannot be created or destroyed. Due to this, she can be converted into other forms of energy, such as kinetic energy and/or gravitational potential energy.
As we can see in the image below, the spring is initially compressed, but when released, it acquires movement due to the transformation of elastic potential energy into kinetic energy.
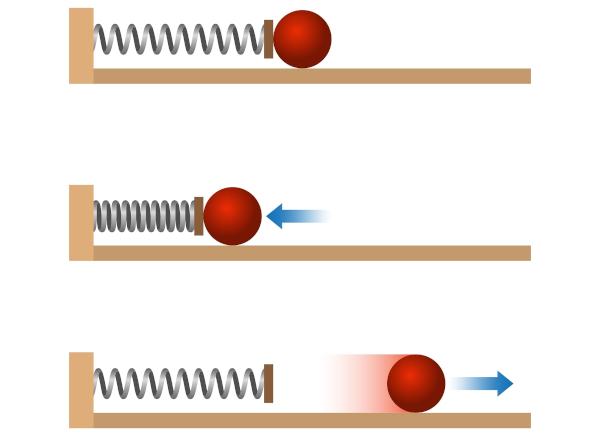
Read too: Conservation of electric charge — the impossibility of creating or destroying charges
Advantage and disadvantage of elastic potential energy
Elastic potential energy has the following advantages and disadvantages:
Advantage: reduces the impact caused by the movement.
Disadvantage: converts energy slowly compared to gravitational potential energy.
Differences between elastic potential energy and gravitational potential energy
Elastic potential energy and gravitational potential energy are forms of potential energy related to different aspects.
Elastic potential energy: associated with the action of springs and elastic objects on bodies.
Gravitational potential energy: associated with the variation in height of bodies that are in a region with gravitational field.
Solved exercises on elastic potential energy
question 1
(Enem) Toy cars can be of several types. Among them, there are rope-powered ones, in which a spring inside is compressed when the child pulls the stroller backwards. When released, the cart starts moving while the spring returns to its initial shape. The energy conversion process that takes place in the cart described is also verified in:
A) a dynamo.
B) a car brake.
C) a combustion engine.
D) a hydroelectric plant.
E) a slingshot (slingshot).
Resolution:
Alternative E
In the slingshot, the elastic potential energy from the spring is converted into kinetic energy, causing the object to be released.
question 2
(Fatec) A block of mass 0.60 kg is dropped from rest at point A on a track in the vertical plane. Point A is 2.0 m above the base of the track, where a spring of spring constant 150 N/m is fixed. The effects of friction are negligible and we adopt \(g=10m/s^2\). The maximum spring compression is, in meters:
A) 0.80
B) 0.40
C) 0.20
D) 0.10
E) 0.05
Resolution:
Alternative B
We will use the theorem of conservation of mechanical energy to find the value of the maximum compression suffered by the spring:
\(E_{m\ before}=E_{m\ after}\)
A mechanical energy is the sum of the kinetic and potential energies, so:
\(E_{c\ before}+E_{p\ before}=E_{c\ after}+E_{p\ after}\)
Where potential energy is the sum of elastic potential energy and gravitational potential energy. So we have:
\(E_{c\ before}+E_{pel\ before}+E_{pg\ before}=E_{c\ after}+E_{pel\ after}+E_{pg\ after}\)
Since, in this case, we have gravitational potential energy converting to elastic potential energy, then:
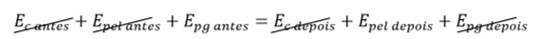
\(E_{pg\ before}=E_{pel\ after}\)
Substituting for their respective formulas, we get:
\(m\cdot g\cdot h=\frac{k\cdot x^2}2\)
\(0,6\cdot 10\cdot 2=\frac{150\cdot x^2}2\)
\(12=75\cdot x^2\)
\(x^2=\frac{12}{75}\)
\(x^2=0.16\)
\(x=\sqrt{0,16}\)
\(x=0.4\m\)
By Pamella Raphaella Melo
Physics Teacher
Source: Brazil School - https://brasilescola.uol.com.br/fisica/energia-potencial-elastica.htm
