Exercises on coefficients and concavity of the parabola

O graph of a function of the 2nd degree, f (x) = ax² + bx + c, is a parabola and the coefficients The, B It is w are related to important features of the parable, such as the concavity.

In addition, the vertex coordinates of a parabola are calculated from formulas involving the coefficients and the value of the discriminating delta.

NGO considers ‘improbable’ federal goal of integral education in the country

Ninth economy on the planet, Brazil has a minority of citizens with…

In turn, the discriminant is also a function of the coefficients and from it we can identify whether or not the 2nd degree function has roots and what they are, if any.

As you can see, from the coefficients we can better understand the shape of a parabola. To understand more, see a list of solved exercises on the concavity of the parabola and the coefficients of the 2nd degree function.

List of exercises on coefficients and concavity of the parabola

Question 1. Determine the coefficients of each of the following functions of the 2nd degree and state the concavity of the parabola.

instagram story viewer

a) f(x) = 8x² – 4x + 1

b) f (x) = 2x² + 3x + 5

c) f (x) = 4x² – 5

e) f (x) = -5x²

f) f (x) = x² – 1

Question 2. From the coefficients of the quadratic functions below, determine the point of intersection of the parabolas with the ordinate axis:

a) f (x) = x² – 2x + 3

b) f (x) = -2x² + 5x

c) f (x) = -x² + 2

d) f (x) = 0.5x² + 3x – 1

Question 3. Calculate the value of the discriminant $\dpi{120} \bg_white \Delta$ and identify whether the parabolas intersect the axis of the abscissas.

a) y = -3x² – 2x + 5

b) y = 8x² – 2x + 2

c) y = 4x² – 4x + 1

Question 4. Determine the concavity and vertex of each of the following parabolas:

a) y = x² + 2x + 1

b) y = x² – 1

c) y = -0.8x² -x + 1

Question 5. Determine the concavity of the parabola, the vertex, the points of intersection with the axes and graph the following quadratic function:

f(x) = 2x² – 4x + 2

Resolution of question 1

a) f(x) = 8x² – 4x + 1

Coefficients: a = 8, b = -4 and c = 1

Concavity: upwards, since a > 0.

b) f (x) = 2x² + 3x + 5

Coefficients: a = 2, b = 3 and c = 5

Concavity: upwards, since a > 0.

c) f (x) = -4x² – 5

Coefficients: a = -4, b = 0 and c = -5

Concavity: down, because a < 0.

e) f (x) = -5x²

Coefficients: a = -5, b = 0 and c = 0

Concavity: down, because a < 0.

f) f (x) = x² – 1

Coefficients: a = 1, b = 0 and c = -1

Concavity: upwards, since a > 0.

Resolution of question 2

a) f (x) = x² – 2x + 3

Coefficients: a= 1, b = -2 and c = 3

The intercept point with the y-axis is given by f (0). This point corresponds exactly to the coefficient c of the quadratic function.

Intercept point = c = 3

b) f (x) = -2x² + 5x

Coefficients: a= -2, b = 5 and c = 0

Intercept point = c = 0

c) f (x) = -x² + 2

Coefficients: a= -1, b = 0 and c = 2

Intercept point = c = 2

d) f (x) = 0.5x² + 3x – 1

Coefficients: a= 0.5, b = 3 and c = -1

Intercept point = c = -1

Resolution of question 3

a) y = -3x² – 2x + 5

Coefficients: a = -3, b = -2 and c = 5

Discriminating:

$\dpi{100} \large \bg_white \Delta b^2 - 4. The. c (-2)^2 - 4.(-3).5 64$

Since the discriminant is a value greater than 0, then the parabola intersects the x-axis at two different points.

b) y = 8x² – 2x + 2

Coefficients: a = 8, b = -2 and c = 2

Discriminating:

$\dpi{100} \large \bg_white \Delta b^2 - 4. The. c (-2)^2 - 4.8.2 -60$

Since the discriminant is a value less than 0, then the parabola does not intersect the x-axis.

c) y = 4x² – 4x + 1

Coefficients: a = 4, b = -4 and c = 1

Discriminating:

$\dpi{100} \large \bg_white \Delta b^2 - 4. The. c (-4)^2 - 4.4.1 0$

Since the discriminant is equal to 0, then the parabola intersects the x-axis at a single point.

Resolution of question 4

a) y = x² + 2x + 1

Coefficients: a= 1, b = 2 and c= 1

Concavity: up, because a > 0

Discriminating:

$\dpi{100} \large \bg_white \Delta 2^2 - 4. 1. 1 4 - 4 0$

Vertex:

$\dpi{100} \large \bg_white x_v \frac{-b}{2a} \frac{-2}{2} -1$

$\dpi{100} \large \bg_white y_v \frac{-\Delta }{4a} 0$

V(-1.0)

b) y = x² – 1

Coefficients: a= 1, b = 0 and c= -1

Concavity: up, because a > 0

Discriminating:

$\dpi{100} \large \bg_white \Delta 0^2 - 4. 1. (-1) 4$

Vertex:

$\dpi{100} \large \bg_white x_v \frac{-b}{2a} 0$

$\dpi{100} \large \bg_white y_v \frac{-\Delta }{4a} \frac{-4}{4} -1$

V(0,-1)

c) y = -0.8x² -x + 1

Coefficients: a= -0.8, b = -1 and c= 1

Concavity: down, because a < 0

Discriminating:

$\dpi{100} \large \bg_white \Delta (-1)^2 - 4. (-0,8). 1 4,2$

Vertex:

$\dpi{100} \large \bg_white x_v \frac{-b}{2a} \frac{1}{-1.6} -0.63$

$\dpi{100} \large \bg_white y_v \frac{-\Delta }{4a} \frac{-4.2}{-3.2} 1.31$

V(-0.63; 1,31)

Resolution of question 5

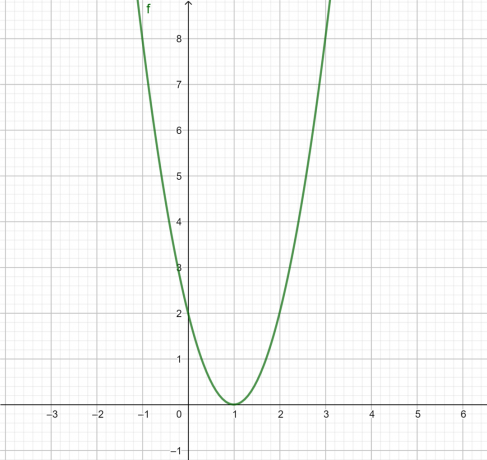
f(x) = 2x² – 4x + 2

Coefficients: a = 2, b = -4 and c = 2

Concavity: up, because a > 0

Vertex:

$\dpi{100} \large \bg_white x_v \frac{-b}{2a}\frac{4}{4} 1$

$\dpi{100} \large \bg_white \Delta (-4)^2 -4. 2. 2 0$

$\dpi{100} \large \bg_white y_v \frac{-\Delta }{4a} 0$

V(1.0)

Intercept with the y-axis:

c = 2 ⇒ dot (0, 2)

Intercept with the x-axis:

As $\dpi{120} \bg_white \Delta 0$ , then the parabola intersects the x-axis at a single point. This point corresponds to the (equal) roots of the equation 2x² – 4x + 2, which can be determined by bhaskara's formula: