The condition of existence of a triangle is a set of relationships between the measures of your sides that make it possible to decide whether, with the proposed measures, it is possible to build it. That condition can be seen as a property and is known as inequalitytriangular.
Condition of existence of a triangle
Dice three straight segments distinct, if the sum of the measurements of two of them is always greater than the measurement of the third, then they can form a triangle.. For example, given the segments AB = 16 cm, CD = 20 cm and EF = 30 cm, it is possible to use them to construct a triangle, as the sums below are true:
16 + 20 = 36 > 30
16 + 30 = 46 > 20
30 + 20 = 50 > 16
Note the triangle which was formed with these three segments in the following figure:
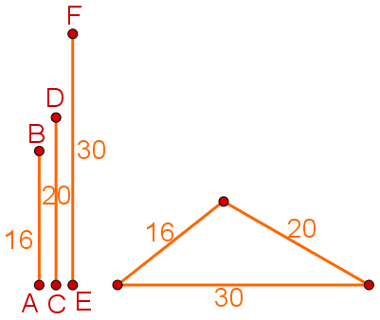
If the sum between the two sides is equal to the third, this triangle cannot exist. Also, the three inequalities above are known as inequalitytriangular.
It is not necessary to make the three sums to check the possibility of a triangle
exist. Just make the sum between the two sides smaller. If the sum between them is greater than the third side, then the sum between any one of them and the third side (which is the greater) will have the same result.Example: A gentleman wants to encircle a triangular plot he owns and argues in a shop that the dimensions of the plot are: 20 m x 15 m x 5 m. Did this gentleman correctly measure his terrain?
The answer is no. how the terrain is triangular, if the measurements were correct, it would be possible to form a triangle. However, these measures do not comply with the inequalitytriangular:
20 + 15 = 35 > 5
20 + 5 = 30 > 15
15 + 5 = 20
Fundamentals of existence condition
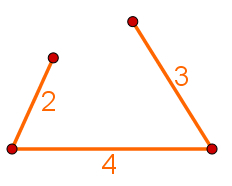
Suppose a person wants to demarcate a piece of land and has only three sticks to do so. She then decides that the markup will have format triangular and that the sides of this triangle will be the same length as the rods. Knowing that they measure 2 meters, 3 meters and 4 meters, it will be possible to build this triangle?
The following image was taken to solve this problem and represents the fixation of the 4-meter rod as the base of the triangle. The ends of the other rods were attached to the ends of the base of the triangle and then rotated the two rods so that they met, as shown in the following diagram:
To see if the free ends of the rods meet so that the triangle is formed, look at the image below, which contains the trajectory of these ends.
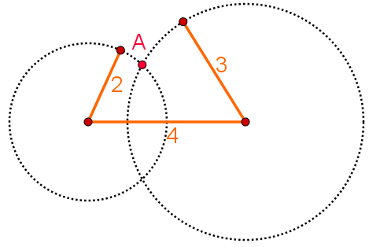
The ends of the rods meet at point A.
Also imagine the same situation as before, only with rods measuring 5 meters, 1 meter and 2 meters. The trajectory of the rods is the same as the following image:
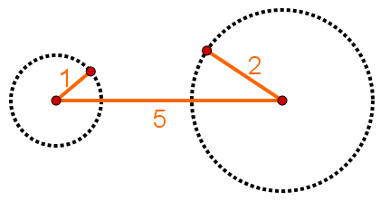
In the image above, notice that there is no possibility to close the triangle with rods that have these measures. In view of these possibilities, the notion of inequalitytriangular.
By Luiz Paulo Moreira
Graduated in Mathematics
Source: Brazil School - https://brasilescola.uol.com.br/o-que-e/matematica/o-que-e-a-condicao-existencia-um-triangulo.htm

