Pythagoras was an important Greek mathematician and philosopher who lived approximately 2500 years ago. He discovered a very interesting relationship involving the size of the sides of right triangles and the area of squares.
remembering:
- A right triangle is any triangle that has a right angle, that is, a 90 degree angle. In the figure below, angle C is straight.
- The side opposite the right angle is called the hypotenuse. In the triangle below, segment AB is the hypotenuse.
- Sides that form a right angle are called legs. In this triangle ABC, segments BC and AC are the legs.

- The area of a square is calculated by multiplying the length of the sides. Thus, if side = a, we have Area = a*a = a².

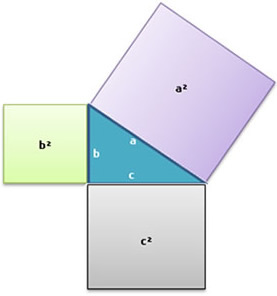
What Pythagoras observed was that in any right triangle, the square of the measure of the hypotenuse is equal to the sum of the leg squares, in other words, the square of the long side measure is equal to the sum of the squares of the side measures minors. So, in the figure below, we can write a²=b²+c². This means that the area of the square of side a (purple) is equal to the area of the square of side b (green) plus the area of the square of side c (gray). This relationship is called the Pythagorean Theorem and the interesting thing is that it is true for any right triangle, regardless of the size of its sides.
by Franciely Guedes
Graduated in Mathematics
Take the opportunity to check out our video lesson related to the subject:

