Observing Pascal's Triangle, it is possible to notice some characteristics that are considered its properties. Among them, the following stand out:
- First and last element of a line.
All lines in Pascal's triangle will have their first and last element equal to 1.
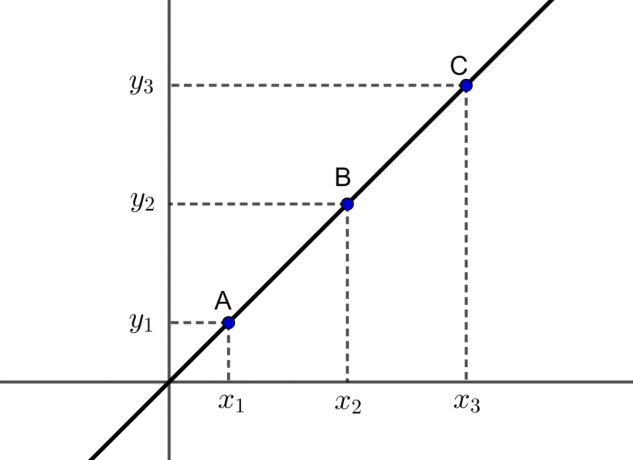
We affirm this because the 1st element of a line is represented by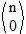 
= 1 and the last is represented by 
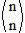= 1. Where n must always be a natural number.
- Proportional elements
This property states that equidistant elements (binomial coefficients) belonging to the same line have equal numerical values. See examples.
Consider the 3rd line: 
Consider the 5th line: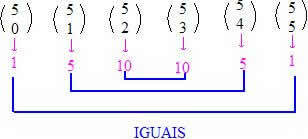 
Do not stop now... There's more after the advertising ;)
- Stifel's relationship.
Considering Pascal's triangle represented by the numerical values of its elements (binomial coefficients), we will notice that the sum of two elements of each line will be equal to the bass element.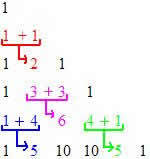 
This property can be represented in the form of an equation: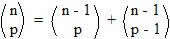 
, taking into account that n is greater than or equal to p.
- Sum of the elements of a line.
The sum of the elements of a row of numerator n will be equal to 2n.
by Danielle de Miranda
Graduated in Mathematics
Brazil School Team
Newton's binomial - Math - Brazil School
Would you like to reference this text in a school or academic work? Look:
DANTAS, James. "Properties of Pascal's Triangle"; Brazil School. Available in: https://brasilescola.uol.com.br/matematica/propriedades-triangulo-pascal.htm. Accessed on June 29, 2021.
