In solving the 2nd degree equation x2 – 6x + 9 = 0, we find two roots equal to 3. Using the decomposition theorem, we factor the polynomial and obtain:
x2 – 6x + 9 = 0 = (x – 3)(x – 3) = (x – 3)2
In this case, we say that 3 is the root of multiplicity 2 or double root of the equation.
Thus, if a factored polynomial results in the following expression: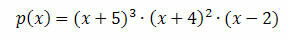
We can say that:
x = -5 is root with multiplicity 3 or triple root of the equation p (x) = 0
x = -4 is root with multiplicity 2 or double root of the equation p (x) = 0
x = 2 is root with multiplicity 1 or simple root of the equation p (x) = 0
In general, we say that r is a root of multiplicity n, with n ≥ 1, of the equation p (x) = 0, if: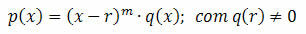
Note that p(x) is divisible by (x – r)m and that the condition q(r) ≠ 0 means that r is not a root of q(x) and guarantees that the multiplicity of the root r is not greater than m.
Example 1. Solve the x equation4 – 9x3 + 23x2 – 3x – 36 = 0, given that 3 is a double root.
Solution: Consider p(x) to be the given polynomial. Thus:
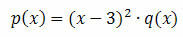
Note that q(x) is obtained by dividing p(x) by (x – 3)2.
By dividing by Briot-Ruffini's practical device, we obtain:
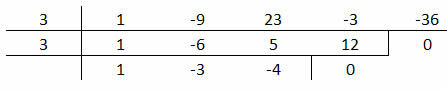
After performing the division, we see that the coefficients of the polynomial q(x) are 1, -3, and -4. Thus, q (x) = 0 will be: x2 – 3x – 4 = 0
Let's solve the equation above to determine the other roots.
x2 – 3x – 4 = 0
Δ = (-3)2 - 4*1*(-4)
Δ = 25
x = -1 or x = 4
Therefore, S = {-1, 3, 4}
Example 2. Write an algebraic equation of minimum degree such that 2 is a double root and – 1 is a single root.
Solution: We have to:
(x – 2)(x – 2 )(x – (-1)) = 0
Or
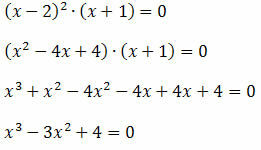
Do not stop now... There's more after the advertising ;)
By Marcelo Rigonatto
Specialist in Statistics and Mathematical Modeling
Brazil School Team
Polynomials - Math - Brazil School
Would you like to reference this text in a school or academic work? Look:
RIGONATTO, Marcelo. "Multiplicity of a root"; Brazil School. Available in: https://brasilescola.uol.com.br/matematica/multiplicidade-uma-raiz.htm. Accessed on June 29, 2021.