In a 1st degree function we have that the rate of change is given by the coefficient a. We have that a 1st degree function respects the following formation law f (x) = ax + b, where a and b are real numbers and b ≠ 0. The rate of change of the function is given by the following expression:
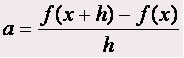
Example 1
Let's go through a demonstration to prove that the rate of change of the function f(x) = 2x + 3 is given by 2.
f (x) = 2x + 3
f (x + h) = 2 * (x + h) + 3 → f (x + h) = 2x + 2h + 3 (h ≠ 0)
So we have to:
f (x + h) − f (x) = 2x + 2h + 3 – (2x + 3)
f (x + h) − f (x) = 2x + 2h + 3 – 2x – 3
f (x + h) − f (x) = 2h
Then:
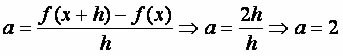
Note that after the demonstration we find that the rate of change can be calculated directly by identifying the value of the coefficient a in the given function. For example, in the following functions the rate of change is given by:
a) f (x) = –5x + 10, rate of change a = –5
b) f (x) = 10x + 52, rate of change a = 10
c) f (x) = 0.2x + 0.03, rate of change a = 0.2
d) f (x) = –15x – 12, rate of change a = –15
Example 2
See one more demonstration proving that the rate of change of a function is given by the slope of the line. The given function is as follows: f (x) = –0.3x + 6.
f (x) = -0.3x + 6
f (x + h) = –0.3(x + h) + 6 → f (x + h) = –0.3x –0.3h + 6
f (x + h) − f (x) = –0.3x –0.3h + 6 – (–0.3x + 6)
f (x + h) − f (x) = –0.3x –0.3h + 6 + 0.3x – 6
f (x + h) − f (x) = –0.3h
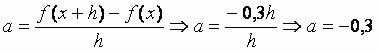
The rate of change of a 1st degree function is determined in higher education courses by developing the derivative of a function. For such application we need to study some fundamentals involving notions of Calculus I. But let's demonstrate a simpler situation involving the derivative of a function. For this, consider the following statements:
The derivative of a constant value is equal to zero. For example:

f (x) = 2 → f’(x) = 0 (read f line)
The derivative of a power is given by the expression:
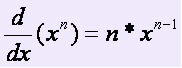
f(x) = x² → f’(x) = 2*x2–1 → f’(x) = 2x
f (x) = 2x³ – 2 → f’(x) = 3*2x3–1 → f’(x) = 6x²
Therefore, to determine the derivative (rate of change) of a 1st degree function, we just apply the two definitions shown above. Watch:
f (x) = 2x – 6 → f’(x) = 1*2x1–1 → f’(x) = 2x0 → f’(x) = 2
f (x) = –3x + 7 → f’(x) = –3
by Mark Noah
Graduated in Mathematics
Brazil School Team
1st Degree Function - Math - Brazil School
Source: Brazil School - https://brasilescola.uol.com.br/matematica/taxa-variacao-funcao-1-o-grau.htm
