Before starting the calculation of inexact roots itself, it is necessary to remember how to calculate roots in general and what exact and non-exact roots are.
calculating roots
Calculating the root of a number boils down to looking for another number that, multiplied by itself a certain number of times, yields the given number.
The representation of roots is done as follows:

*no, called the index, is the number of factors of the power that generated The, called radicando, and L is the result, called the root.
Thus, L is a number that has been multiplied by itself no times and the result of this multiplication was The.
L·L·L·L...L·L = a
Exact and Inexact Roots
We say that a root is exact when L is an integer. Some examples of exact roots are:
a) The square root of 9, since 3·3 = 9
b) The cubic root of 8, since 2·2·2 = 8
c) The fourth root of 16, since 2·2·2·2 = 16
However, when it is not possible to find an integer that is the root of a number, then this root it's not exact. They all belong to the set of irrational numbers and therefore they are all infinite decimals. Some examples of inexact roots are:
a) Square root of 2
b) Cubic root of 3
c) Fourth root of 5
Calculation of inexact roots
Case 1 - Rooting cousin
If the radicand belongs to the set of prime numbers, it is necessary to look for approximate values for its root. This calculation is done by looking for exact roots close to the radicand and, later, approaching the root of the radicand based on the closest exact root. For example, let's calculate the cubic root of 31:

In the previous image, we saw that the cubic root of 31 has a decimal result between 3 and 4. To find an approximation of L, it is necessary to define how many decimal places it should have and look for the number that, cubed, comes closest to 31. In the example, we will use an approximation to two decimal places. Therefore, L = 3.14, because:
3,143 = 30,959144
Case 2 - Rooting non-cousin
When the radicand is not prime, decompose it into prime factors and group these factors into powers whose exponent is equal to the index of the radicand. This will allow immediate calculation of all factors whose exponent is equal to the index and will summarize the calculations to roots of the smallest possible prime numbers for that root.
Example:
Knowing that the cubic root of 2 is approximately 1.26, calculate the cubic root of 256. In other words, calculate:

Solution: First, get the prime factor decomposition of 256:
256|2
128|2
64|2
32|2
16|2
8|2
4|2
2|2
1
256 = 23·23·22
Now, regroup the factors into powers of exponent 3 within the radical. Watch:
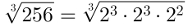
Finally, it is possible to use one of the radical properties to simplify the root above. Therefore, rewrite the equality as follows to get the indicated result:

To find the numerical value of the above expression, note that the result is a cubic root of 2 squared. We can rewrite it as follows:
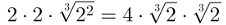
Replace the cubic roots of 2 with the value given in the exercise and perform multiplication.
4·1,26·1,26 = 6,35
By Luiz Paulo Moreira
Graduated in Mathematics
Source: Brazil School - https://brasilescola.uol.com.br/matematica/calculo-raizes-nao-exatas.htm

