To understand the sum of two cubes, It is important to understand that we use the product of two polynomials to facilitate operations and simplifications. at work with polynomials, it becomes necessary to know how to factor them, and finding factorization is looking for a way to represent the polynomial as the product of two or more polynomials. Knowing how to apply the factorization of this polynomial is essential to simplify problem situations involving the sum of two cubes. There is a formula used to carry out this factorization.
Read too: How to simplify an algebraic fraction?

How is the sum of two cubes factored?
THE factoring a polynomial is quite common in Mathematics and its purpose is to express this polynomial as the product of two or more polynomials. From this representation, it is possible to carry out simplifications and solve situations that involve, in this case, the sum of two cubes. To carry out the factorization, it is necessary to know the formula for the sum of two cubes.
Formula of the sum of two cubes
Consider The as the first term and B as the second term and they can be any real number, so we have to:
a³ + b³ = (a+b)(a² - ab +b²)
Analyzing the second member of the equation, we will show that by applying the distributive property, we can find the first member.
(a+b)(a² - ab +b²) = a³ – a²b+ab²+a²b–ab² +b³
Note that the terms in red and the terms in blue are respectively opposite, so their sum is equal to zero, leaving:
(a+b)(a² - ab +b²) = a³ + b³
To perform the factorization of the difference cube, let's apply the formula and find the terms a and b, as shown in the following example.
Example 1:
Solve x³ + 27.
Rewriting the equation, we know that 27=3³, so let's represent it by: x³ + 3³ → sum of two cubes, where x is the first term and 3 is the second term.
Performing factorization using the formula, we have to:
x³ + 3³ = (x+3)(x² - x·3 +3²)
x³ + 3³ = (x+3)(x² - 3x +9)
Therefore, the factorization of x³ + 27 is equal to (x+3)(x² – 3x +9).
Example 2:
Solve 8x³ + 125.
Rewriting the equation, we know that 8x³ = (2x) ³ and 125=5³, so let's represent by: (2x) ³ + 5³ → sum of two cubes, where 2x is the first term and 5 is the second term.
Performing factorization using the formula, we have to:
(2x) ³ + 5³ = (2x +5) ((2x) ² – 2x·5+5²)
(2x) ³ + 5³ = (2x+5) (4x² – 10x +25)
Therefore, the factorization of 8x³ + 125 is equal to (2x+5)(4x² – 10x +25).
See too: How to add and subtract algebraic fractions?
solved exercises
Question 1 - Knowing that a³ + b³ = 1944 and that a+b = 1 and ab = 72, the value of a²+b² is ?
A) 160
B) 180
C) 200
D) 240
E) 250
Resolution
Alternative B.
Let's factor out a³ + b³.
a³ +b³ = (a+b) (a² - ab + b²)
Now we will use the question data replacing a+b, ab and a³ + b³:
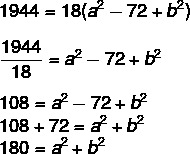
Question 2 - The simplification of the expression is:
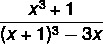
TO 1
B) x+1
C) -3xy
D) x² + y²
E) 5
Resolution
Alternative A.
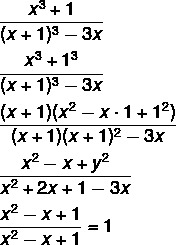
By Raul Rodrigues de Oliveira
Maths teacher
Source: Brazil School - https://brasilescola.uol.com.br/matematica/soma-dois-cubos.htm
