To graphically locate the images formed from a lens, we will use the combination of three 'magical' rays.
1. A ray parallel to the central axis, which after being refracted by the lens passes through the focal point F’.
2. A ray that passes through the focal point F and after being refracted becomes parallel to the central axis.
3. A ray that passes through the center of the lens emerges from the lens without changing direction, as it crosses a region where the two sides are practically parallel.
The point image is at the intersection of two chosen radii. To determine the image of the complete object, just find the location of two or more of its points.
The equations for spherical lenses are:
Gaussian Equation: 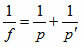
Transverse linear increase equation 
Example:
A real object 30 cm high is placed 24 cm from a converging lens of focal length f = 6 cm. Determine the image position, image height and transverse linear magnification.
To make it easier to solve the problem, sketch a figure using the magic rays to form the image:
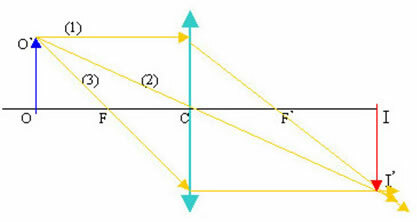
Remove the problem data:
Data: p = 24cm
O = 30 cm
f = 6 cm
Thus, using the Gauss equation we have:

Where p’ is the position of the image.
To find the height of the image, we will use the transversal linear increase equation.
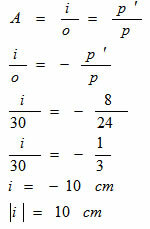
The linear magnification of the image is:
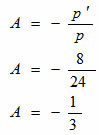
By Kleber Cavalcante
Graduated in Physics
Brazil School Team
Optics - Physics - Brazil School
Source: Brazil School - https://brasilescola.uol.com.br/fisica/construcao-imagens-produzidas-por-lentes.htm

