the set of Prime numbers is the object of study in math from Ancient Greece. Euclides, in his great work “The elements”, was already discussing the subject, managing to demonstrate that this set is infinite. As we know, the prime numbers are those that have the number 1 as a divisor and themselves, thus, finding very large primes is not an easy task, and Eratosthenes' sieve makes it easy. meeting.

How do you know when a number is prime?
We know that a prime number is awhoever has as divider the number 1 and himself, so a number that, in its list of divisors, has numbers other than 1 and of itself will not be prime, see:
By listing the 11 and 30 dividers, we have:
D(11) = {1, 11}
D(30) = {1, 2, 3, 5, 6, 10, 30}
Note that the number 11 has only the number 1 and itself as divisors, so the number 11 is a prime number. Now, look at the divisors of the number 30, it has, in addition to the number 1 and itself, the numbers 2, 3, 5, 6 and 10 with divisors. Therefore, the number 30 is not prime.
→ Example: List the primes less than 15.
For this, we will list the divisors of all numbers between 2 and 15.
D(2) = {1, 2}
D(3) = {1,3}
D(4) = {1, 2, 4}
D(5) = {1, 5}
D(6) = {1, 2, 3, 6}
D(7) = {1, 7}
D(8) = {1, 2, 4, 8}
D(9) = {1, 3, 9}
D(10) = {1, 2, 5, 10}
D(11) = {1, 11}
D(12) = {1, 2, 3, 4, 6, 12}
D(13) = {1, 13}
D(14) = {1, 2, 7, 14}
D(15) = {1, 3, 5, 15}
Thus, primes smaller than 15 are:
2, 3, 5, 7, 11 and 13
Let's face it, this task wouldn't be very pleasant, for example, if we were to write down all the primes between 2 and 100. To avoid it, we will learn to use, in the next topic, the sieve of Eratosthenes.
Sieve of Eratosthenes
The sieve of Eratosthenes is a tool that aims to facilitate the determination of prime numbers. The sieve consists of four steps, and it is necessary, in order to understand them, to keep in mind the divisibility criteria. Before starting the step by step, we must create a table from the number 2 to the desired number, since the number 1 is not prime. Then:
→ Step 1: From the divisibility criterion by 2, we have that the even numbers are all divisible by it, that is, the number 2 will appear in the list of divisors, so these numbers will not be prime and we must exclude them from the table. Are they:
4, 6, 8, 10, 12, 14, …, 1000, 1002, 1004, …
→ Step 2: From the criterion of divisibility by 3, we know that a number is divisible by 3 if the sum of its digits it is also. Thus, we must exclude these numbers from the table, as they are not prime because there is a number other than 1 and itself in the list of divisors. So, we must exclude the numbers:
6, 9, 12, 15, 18, …, 2133, 2136, …
→ Step 3: From the criterion of divisibility by 5, we know that all numbers ending in 0 or 5 are divisible by 5, so we must exclude them from the table.
10, 15, 20, 25, …, 655, 670,…
→ Step 4: Similarly, we must exclude numbers that are multiples of 7 from the table.
14, 21, 28, …, 546, …
– Knowing the sieve of Eratosthenes, let's determine the primes between 2 and 100.
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
21 |
22 |
23 |
24 |
25 |
26 |
27 |
28 |
29 |
30 |
31 |
32 |
33 |
34 |
35 |
36 |
37 |
38 |
39 |
40 |
41 |
42 |
43 |
44 |
45 |
46 |
47 |
48 |
49 |
50 |
51 |
52 |
53 |
54 |
55 |
56 |
57 |
58 |
59 |
60 |
61 |
62 |
63 |
64 |
65 |
66 |
67 |
68 |
69 |
70 |
71 |
72 |
73 |
74 |
75 |
76 |
77 |
78 |
79 |
80 |
81 |
82 |
83 |
84 |
85 |
86 |
87 |
88 |
89 |
90 |
91 |
92 |
93 |
94 |
95 |
96 |
97 |
98 |
99 |
100 |
→ are not cousins
→ Prime numbers
So the prime numbers between 2 and 100 are:
{2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97}
Read too: MMC and MDC calculation: how to do it?
Prime factor decomposition
THE prime factor decomposition is formally known as fundamental theorem of arithmetic. This theorem states that any integer different from 0 and greater than 1 can be represented by the product of prime numbers. To determine the factored form of an integer, we must perform successive divisions until we reach the result equal to 1. See the example:
→ Determine the factored form of the numbers 8, 20 and 350.
To factor the number 8, we must divide it by the first possible prime number, in this case by 2. Then, we perform another division also by the prime that is possible, this process is repeated until we reach the number 1 as the answer to the division. Look:
8: 2 = 4
4: 2 = 2
2: 2 = 1
Therefore, the factored form of the number 8 is 2 · 2 · 2 = 23. In order to facilitate this process, we will adopt the following method:

Therefore, the number 8 can be written as: 23.
→ To factor the number 20, we will use the same method, that is: divide it by prime numbers.
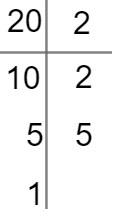
So the number 20, in its factored form, is: 2 · 2 · 5 or 22 · 5.
→ Similarly, we will do with the number 350.
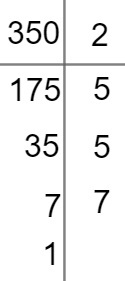
Therefore, the number 350, in its factored form, is: 2 · 5 · 5 · 7 or 2 · 52 · 7.
See too: Scientific notation: what is it for?
solved exercises
question 1 – Simplify the expression:
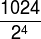
Solution
First, let's factor the expression to make it easier.

Thus, 1024 = 210, and therefore we can substitute one for the other in the exercise expression. Thus:
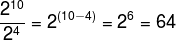
by Robson Luiz
Maths teacher
Source: Brazil School - https://brasilescola.uol.com.br/matematica/numeros-primos.htm
