A geometric progression is a numerical sequence that respects a formation law. In a PG, every term, starting from the second, is obtained by making the product between the previous term and a constant q. This constant q is called the geometric progression ratio. Interpolate geometric means between any two numbers a1 and theno means to determine the real numbers existing between the1 and theno so that the number sequence is a PG.
To perform the interpolation of geometric means we need to use the general term formula of PG: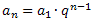
To interpolate geometric means, it is also necessary to know the value of the PG ratio.
Example 1. A PG is formed by 6 terms, where the1 = 4 and the6 = 972. Determine the geometric means existing between the1 and the6.
Solution: To interpolate the geometric means between 4 and 972 we need to determine the value of the PG ratio. For this, we will use the general term formula.
We know that the ratio of PG is 3 and that each term, starting from the second, is obtained by making the product between the previous term and the ratio. Thus, we will have:
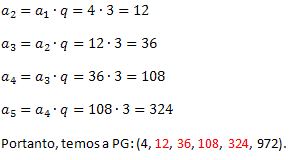
Example 2. Determine the missing terms in the number sequence (3, _, _, _, _, _, _, _, _, 1536) so that we have a geometric progression.
Solution: Note that finding the missing terms in the sequence with endpoints 3 and 1536 means to interpolate geometric means. Thus, we need to determine the value of the ratio of this PG.
From the numerical sequence given, we know that the1 = 3 and the10 = 1536 (since 1536 occupies the tenth position in the sequence). Using the general term formula, we will have:
Once the value of the ratio is known, we can determine the terms that are missing in the sequence:
Example 3. An industry produced 100 units of a product in January. In July of the same year, it produced 6400 units of this product. Determine how many units were produced in the months of February to June, knowing that quantities produced from January to July determine a PG.
Solution: According to the problem statement, the sequence (100, _, _, _, _, _, 6400) is a PG. To solve the problem we need to determine the missing terms in this PG or interpolate geometric means between 100 and 6400. So we need to determine the reason for this PG, where the1 = 100 and the7 = 6400.
Knowing the value of reason, we have to:
Therefore, production in the month of February was 200 units; March was 400 units; April was 800 units; May was 1600 units; and June was 3200 units.
By Marcelo Rigonatto
Specialist in Statistics and Mathematical Modeling
Brazil School Team
Progressions - Math - Brazil School
Source: Brazil School - https://brasilescola.uol.com.br/matematica/interpolacao-meios-geometricos.htm
