THE injection function, also known as the injective function, is a particular case of function. For a function to be considered injecting, we must have the following occurrence: given two elements, x1 and x2, belonging to the domain set, with x1 different from x2, images f(x1) and f(x2) are always distinct, that is, f(x1) ≠ f(x2). This function has specific characteristics that enable the identification of its graph and also the analysis of the formation law.
Read too: Domain, contra-domain and image - basic terms for understanding the content of functions
What is an injection function?
To build some examples of injector function, it is important to understand the definition of this type of function. A function f: A → B is classified as injecting if, and only if, elements different from set A have different images in set B, i.e:
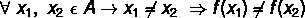
Example 1:
Below is an example of injector function in dve diagramnono:
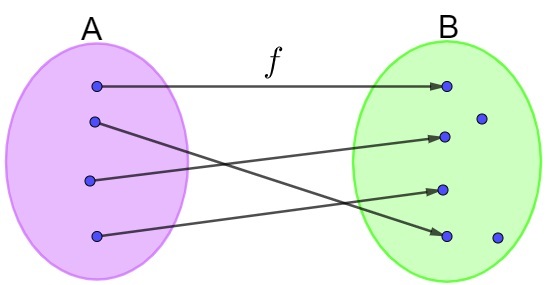
Example 2:
Below is an example of a non-injecting function. Note that in the
set A, there are two distinct elements that have the same image in set B, which contradicts the definition of injector function.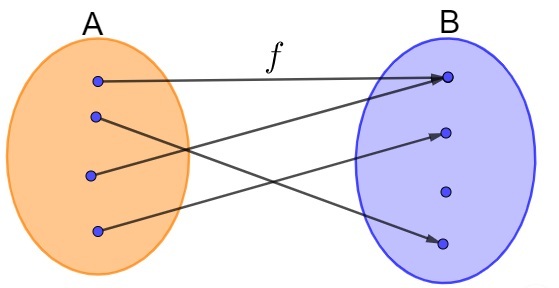
How to calculate an injector function?
To verify whether a function is injecting or not, it is necessary to analyze the behavior of the formation law and also the domain and counter-domain in which the function is defined.
Example:
given the function f: R → R, with the formation law f(x) = 2x, check if it is injector.
By the formation law, we can see that it takes a real number of the domain and turns it into its double. Two distinct real numbers, when multiplied by two, yield distinct results. THE occupationf, as we can see, it is an injector function, since for any two values of x1 and x2,the value of f(x1) ≠ f(x2).
Example 2:
given the function f: R → R, with formation law f(x) = x², check if it is injector.
We can observe that, for this domain, this function is not injecting, as we have that the image of any number is equal to the image of its opposite, for example:
f( 2) = 2² = 4
f( --2 ) = (– 2) ² = 4
note that f(2) = f ( – 2), which contradicts the definition of an injector function.
Example 3:
given the function f:R+ → R, with formation law f(x) = x², check if it is injector.
Note that now the domain is the positive real numbers and zero. The function turns the real number into its square; in this case, when the domain is the set of positive real numbers, this function is injective, as the square of two distinct positive numbers will always generate distinct results. So, it is very important to remember that, in addition to the function formation law, we need to analyze its domain and counter-domain.
Read too: What is an inverse function?
Injection Function Chart
To identify whether the graph is an injector function or not, just check if there are two distinct x-values that generate the same y-correspondent, that is, check the validity of the definition of injector function.
In the range where we are going to look at the graph, the function has to be exclusively increasing or exclusively decreasing. Graphics like the parable or the sine function are not graphs of injector functions.
Example 1:
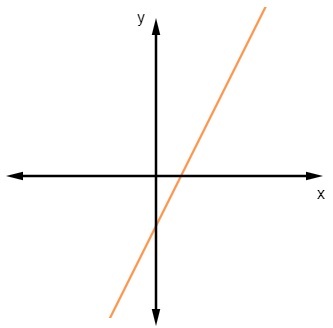
The rising line is the graph of an injection function. Note that it is always increasing and that there is no y-value that has two distinct correspondents.
Example 2:
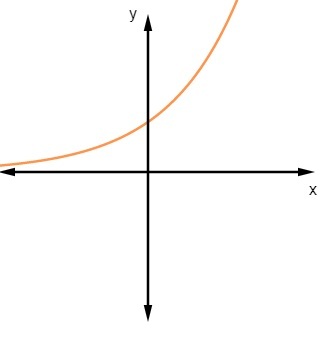
The graph of a exponential function it is also the graph of an injector function.
Example 3:
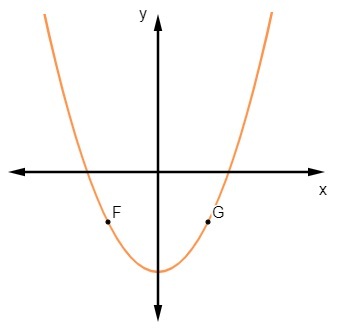
The graph of a quadratic function it is always a parable. When the domain involves the real numbers, it is possible to see that there are different x values that have the same corresponding in y, as in points F and G, which makes this graph of a function that is not injector.
In summary, to know if the graph is or not of an injector function, it is enough to check if the definition of an injector function is valid or not for that function.

solved exercises
Question 1 - (Enem 2017 – PPL) In the first year of high school at a school, it is customary for students to dance square dances at the June party. This year, there are 12 girls and 13 boys in the class, and 12 different pairs were formed for the gang, consisting of a girl and a boy. Assume that girls are the elements that make up set A and boys, set B, so that the pairs formed represent a function f from A to B.
Based on this information, the classification of the type of function that is present in this relationship is
A) f is injecting, because for each girl belonging to set A, a different boy belonging to set B is associated.
B) f is surjective, since each pair is formed by a girl belonging to set A and a boy belonging to set B, leaving an unpaired boy.
C) f is injecting, as any two girls belonging to set A pair with the same boy belonging to set B, to involve all students in the class.
D) f is bijective, since any two boys belonging to set B form a pair with the same girl belonging to set A.
E) f is surjective, as it is enough for a girl from set A to form a pair with two boys from set B, so that no boy will be without a pair.
Resolution
Alternative A.
This function is injective because, for each element of set A, there is a single correspondent in set B. Note that there is no possibility of two girls dancing with the same pair, so this relationship is injecting.
Question 2 - (IME - RJ) Consider the sets A = {(1,2), (1,3), (2,3)} and B = {1, 2, 3, 4, 5}, and let the function f: A → B such that f(x, y) = x + y.
It is possible to say that f is a function:
A) injector.
B) surjective.
C) bijector.
D) par.
E) odd.
Resolution
Alternative A.
Analyzing the domain, we have to:
f (1.2) = 1 + 2 = 3
f (1,3) = 1 + 3 = 4
f(2,3) = 2 + 3 = 5
Note that for any two distinct terms in the domain, they are related to distinct terms in the counterdomain, which makes this function an injector.
By Raul Rodrigues de Oliveira
Maths teacher
Source: Brazil School - https://brasilescola.uol.com.br/matematica/funcao-injetora.htm

