Circular crown area

Consider a circle inscribed on another circle, that is, two concentric circles (same center), the flat region delimited by them is called a circular crown.
See illustrations below:

Thus, we will have two radii: one from the largest circumference and one from the smallest.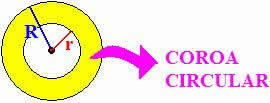

From the figure we can say that the area of ​​the circular crown will be equal to the difference in the area of ​​the two circles that form the crown:
THE_crown = A_{bigger circle} - A_{smaller circle}
THE_crown = (π. R2) - (π. r2)
THE_crown = π. (R2 - r2)
Example: Determine the colored surface area:

AC = AO/2
AO = 10
As the colored region is 1/4 of the circular crown, we will have to divide the total area of ​​the crown by 4:
THE_colorful = π (R2 - r2)
4

THE_colorful = π (152 - 102)
4

THE_colorful = π (225 – 100)
4

THE_colorful = π 125
4

THE_colorful = 125π cm²
4
Example: The colored region in the figure below is 32 π/25 m² of area. If the radius of the arc measures 4m, how much is the radius of the smallest?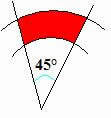

360°: 45° = 8, this means that the painted part corresponds to 1/8 of the circular crown, so we can say that the crown will have an area equal to:

THE_crown = 32 π/25. 8 = 256 π / 25
To find out the value of the smallest radius, just apply the formula and make the necessary substitutions:
THE_crown = π. (R2 - r2)
256 π / 25 = π. (42 - r2)
256 π / 25 = π. (16 - r2)
10.24 = 16 - r2
10.24 – 16 = – r2 (-1)
-10.24 + 16 = r2
5.76 = r2
2.4 = r

by Danielle de Miranda
Graduated in Mathematics
Brazil School Team

Spatial Metric Geometry - Math - Brazil School

Source: Brazil School - https://brasilescola.uol.com.br/matematica/area-coroa-circular.htm