We define a polygon as a closed polygonal line, it is classified as flat and not flat, see the examples:
Flat
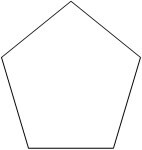
I don't plan
These closed polygonal lines are also called straight lines. See some more examples of line segments that form polygons:

Polygons are classified into convex and non-convex. What makes these two classifications different is the line segment formed by the union of two points belonging to the surface (region delimited by the polygon) of the polygon. If this line segment belongs only to the region bounded by the polygon, it will be convex; otherwise it will be non-convex.
Mind Map: Polygons
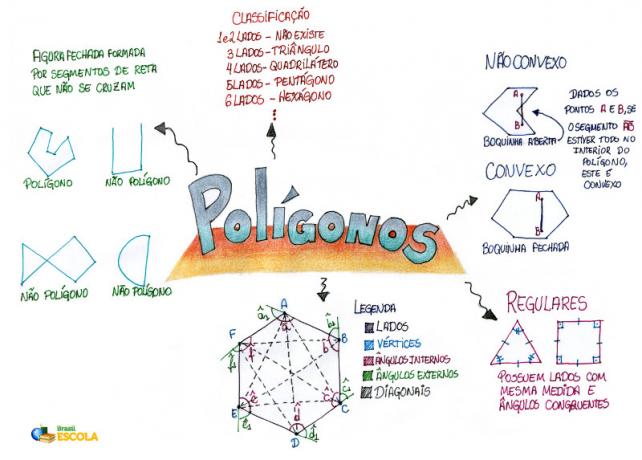
*To download this mind map in PDF, Click here!
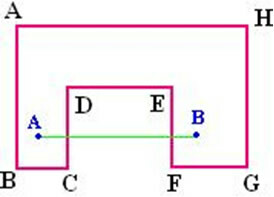
Note the ABCD polygon, it is a typical example of a convex polygon. When tracing a line segment in its interior, we verify that all points remain located in the internal region of the polygon.

The following figure is an example of a non-convex polygon. In this polygon, when we trace a line segment inside it, we notice that in certain positions some points are located in the external region.
In flat and convex polygons, closed polygonal lines are called sides. The point that represents the meeting of the sides of a polygon is called a vertex. Note the following polygon:
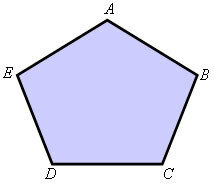
The vertices of the polygon are given by the points: A, B, C, D and E.
The sides of the polygon are represented by the line segments: AB, BC, CD, DE, and EA.
In a polygon we still have the existence of other elements, such as internal angles, external angles and diagonals.
The internal and external angles are formed by the meeting of the sides, and the diagonals, by segments of straight lines that connect one vertex to the other of the polygon. Watch:

by Mark Noah
Graduated in Mathematics
*Mental Map by Luiz Paulo Silva
Graduated in Mathematics
Source: Brazil School - https://brasilescola.uol.com.br/matematica/tipos-poligonos.htm
