Several aspects can be analyzed to define if one figure is similar to another. For example, in triangles, there are at least four cases of congruence. But, in general, it is possible to say that two or more figures are similar if they have the same angles, the same number of sides and some proportion between the measurements of the sides. An alternative presented for the construction of similar figures is the homothety.
Homothety is a type of geometric transformation that took a back seat when the subject was similarity of figures. However, it is a strong ally for the enlargement or reduction of geometric figures. In general, when applying dilation to a drawing, the main features, such as shape and angles, are preserved; but the size of the figure changes. This relationship can be explained through the Greek derivation of the word homothetia, in which homos means equal, and thetos, placed, that is, the homothetic figures are placed at a distance equal to “something”. Copying machines that make enlargements or reductions generally use homothety as a principle in their operation. Let's see a little more about homothetic figures below:
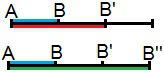
Relation of dilation between segments AB, AB' and AB''
In the figure above, there is a segment AB from which you want to create a segment starting from A that has twice that segment. To do this, create the segment AB', highlighted in red in the figure above. Thus, it can be said that:
AB' = 2. AB or yet
AB = 1
AB' 2
In this case, there is an A-centered homothety. Point B' is called Image (or homothetic) from point B.
If you wanted to trace a new segment that had triple the initial segment, there would be the segment AB'', highlighted in green in the figure, which would correspond to triple the length of AB. Therefore, among these segments there would be the following reason:
AB'' = 3. AB or yet
AB = 1
AB'' 3
In this case, there is a dilation centered on A, and point B'' is the image of point B or the homothetic of point B.
Is it possible to establish a relationship between AB' and AB''? if AB' = 2. AB and AB'' = 3. AB, soon:
AB' = 2. AB → AB = 1 . AB'
2
AB'' = 3. AB → AB = 1 . AB''
3
Therefore:
1 . AB' = 1 . AB''
2 3
AB' = 2 . AB''
3
The ratio between the segments AB' and AB'' it's from ⅔.
Now look at a dither ratio for enlarging a hexagon. Starting from center A, there is a ratio 3 dilation, because the length of the segment AB' is triple the segment AB. It is possible to see that the reason is preserved in relation to all the other vertices of the hexagon. Although the hexagon did not change its initial shape, the measurement of its sides increased three times, but its internal angles remained unchanged.
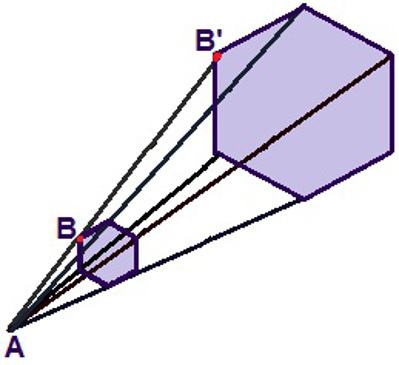
Through a dilation relationship, we can guarantee that the hexagons are similar, but the largest is three times the size of the smallest
By Amanda Gonçalves
Graduated in Mathematics
