O sphere volume is the space occupied by this geometric solid. Through the ray of ball — that is, from the distance between the center and the surface — it is possible to calculate its volume.
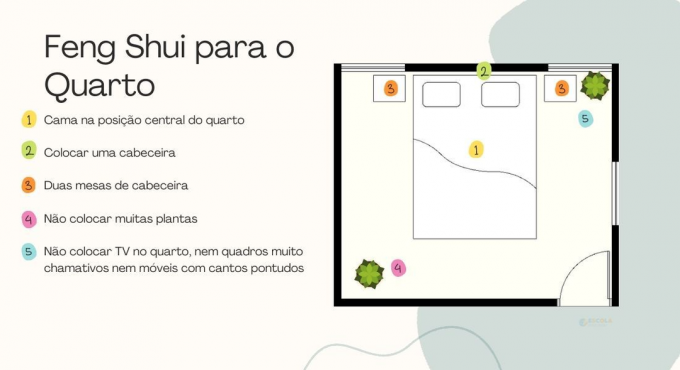
Read too: Volume of geometric solids
Summary about the volume of the sphere
The sphere is a round body obtained by revolving a semicircle around an axis containing the diameter.
All points on a sphere are at a distance equal to or less than r from the center of the sphere.
The volume of the sphere depends on the measure of the radius.
The formula for the volume of the sphere is \(V=\frac{4·π·r^3}3\)
Video lesson on the volume of the sphere
What is sphere?
Consider a point O in space and a segment with measure r. the sphere is the solid formed by all points that are at a distance equal to or less than r from O. We call O the center of the sphere and r the radius of the sphere.

the sphere can also be characterized as a solid of revolution. Note that rotating a semicircle about an axis containing its diameter forms a sphere:

Sphere volume formula
To calculate the volume V of a sphere, we use the formula below, where r is the radius of the sphere:
\(V=\frac{4·π·r^3}{3}\)
It is important to observe the unit of measurement radius to determine the unit of measure for volume. For example, if r is given in cm, then the volume must be given in cm³.
How to calculate the volume of the sphere?
The calculation of the volume of the sphere depends only on the measurement of the radius. Let's look at an example.
Example: Using the approximation π = 3, find the volume of a basketball that is 24 centimeters in diameter.
Since the diameter is twice the radius, r = 12 cm. Applying the formula for the volume of the sphere, we have
\(V=\frac{4·π·12^3}3\)
\(V=\frac{4 · π·1728}3\)
\(V=6 912\ cm^3\)
sphere regions
Consider a sphere with center O and radius r. Like this, we can consider three regions of this sphere:
The inner region is formed by the points whose distance from the center is less than the radius. If P belongs to the inner region of the sphere, then
\(D(P, O)
The surface region is formed by the points whose distance from the center is equal to the radius. If P belongs to the surface region of the sphere, then
\(D(P, O)=r\)
The outer region is formed by the points whose distance from the center is greater than the radius. If P belongs to the inner region of the sphere, then
\(D(P, O)>r\)
Consequently, points on the outer region of the sphere do not belong to the sphere.
Know more: Spherical cap — solid obtained when a sphere is intersected by a plane
Other sphere formulas
A sphere area — that is, the measurement of its surface — also has a known formula. If r is the radius of the sphere, its area A is calculated by
\(A=4·π·r^2\)
In this case, it is also important to note the unit of measurement for the radius to indicate the unit of measurement for the area. For example, if r is in cm, then A must be in cm².
Solved exercises on the volume of the sphere
question 1
What is the radius of a sphere that has a volume of 108 cubic centimeters? (Use π = 3).
a) 2 cm
b) 3 cm
c) 4 cm
d) 5 cm
e) 6 cm
Resolution
Alternative B.
Consider that r is the radius of the sphere. Knowing that V = 108, we can use the formula for the volume of the sphere:
\(V=\frac{4·π·r^3}3\)
\(108=\frac{4·3·r^3}3\)
\(108=4·r^3\)
\(r^3=27\)
\(r = 3\ cm\)
question 2
An ancient spherical reservoir is 20 meters in diameter and has a volume V1. It is desired to build a second reservoir, of volume V2, with twice the volume of the old reservoir. So, V2 it's the same as
The) \(\frac{3000·π}{8} m^3\)
B) \(\frac{3000·π}{4} m^3\)
w) \(\frac{2000·π}{3} m^3\)
d) \(\frac{4000·π}{3} m^3\)
It is) \(\frac{8000·π}{3} m^3\)
Resolution
E alternative.
As the diameter is twice the radius, the old reservoir has radius r = 10 meters. Therefore
\(V_1=\frac{4·π·r^3}3\)
\(V_1=\frac{4·π·10^3}3\)
\(V_1=\frac{4000·π}3\ m^3\)
By the statement, \(V_2=2·V_1\), i.e
\(V_2=\frac{8000·π}3 m^3\)
By Maria Luiza Alves Rizzo
Math teacher
Source: Brazil School - https://brasilescola.uol.com.br/matematica/volume-da-esfera.htm